Giúp e vơi ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`1+1/3=4/3`
`=>1/(1+1/3)=1:4/3=3/4`
`=>B=(1-1/3+3/4)/(1-1/3-3/4)`
`=(2/3+3/4)/(2/3-3/4)`
`=17/12:(-1/12)`
`=-17`

\(\overrightarrow{AB}=\left(1;1\right)\Rightarrow AB=\sqrt{2}\)
Từ C hạ CH vuông góc AB \(\Rightarrow S_{ABC}=\dfrac{1}{2}CH.AB\Rightarrow CH=\dfrac{2S_{ABC}}{AB}=\dfrac{3}{\sqrt{2}}\)
Từ G hạ GK vuông góc AB, gọi M là trung điểm AB
Theo định lý Talet: \(\dfrac{GK}{CH}=\dfrac{GM}{CM}=\dfrac{1}{3}\Rightarrow d\left(G;AB\right)=GK=\dfrac{CH}{3}=\dfrac{\sqrt{2}}{2}\)
Phương trình AB có dạng:
\(1\left(x-2\right)-1\left(y+3\right)=0\Leftrightarrow x-y-5=0\)
G thuộc d nên tọa độ có dạng: \(G\left(a;3a-8\right)\)
\(d\left(G;AB\right)=\dfrac{\sqrt{2}}{2}=\dfrac{\left|a-\left(3a-8\right)-5\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left|-2a+3\right|=1\Rightarrow\left[{}\begin{matrix}a=1\\a=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}G\left(1;-5\right)\\G\left(2;-2\right)\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x_C=3x_G-\left(x_A+x_B\right)=...\\y_C=3y_G-\left(y_A+y_B\right)=...\end{matrix}\right.\)

Gọi số đó là \(\overline{abcd}\)
TH1: \(a=2\)
- Nếu \(b=0\Rightarrow c\) có 4 cách chọn (3;4;5;6), d có 4 cách chọn
- Nếu \(b\ne0\Rightarrow b\) có 5 cách chọn, c có 5 cách, d có 4 cách
\(\Rightarrow4.4+5.5.4=116\) số
TH2: \(a>2\Rightarrow a\) có 4 cách chọn
Bộ bcd có \(A_6^3=120\) cách
Tổng cộng có:
\(116+4.120=596\) số

Kẻ AK vuông góc SC
BC vuông góc (SAC)
=>BC vuông góc AK
=>d(A;(SBC))=AK
SC=căn SA^2+AC^2=2a
=>AK=a*a*căn 3/2a=a*căn 3/2

1
a
\(A=x^2-2x+4=x^2-2x+1+3\\=\left(x-1\right)^2+3\ge3\)
Min A = 3 khi và chỉ khi `x=1`
b
\(B=x^2+4x+5=x^2+4x+4+1\\ =\left(x+2\right)^2+1\ge1\)
Min B = 1 khi và chỉ khi `x=-2`
c
\(C=x^2+3x+4=x^2+3x+\dfrac{9}{4}+\dfrac{7}{4}\\ =\left(x+\dfrac{3}{2}\right)^2+\dfrac{7}{4}\ge\dfrac{7}{4}\)
Min C = \(\dfrac{7}{4}\) khi và chỉ khi \(x=-\dfrac{3}{2}\)
d
\(D=3x^2-6x+4=3\left(x^2-2x+\dfrac{4}{3}\right)\\ =3\left(x^2-2x+1+\dfrac{1}{3}\right)\\ =3\left(x-1\right)^2+3.\dfrac{1}{3}\ge3.\dfrac{1}{3}\)
Min D = 1 khi và chỉ khi `x=1`

1. There are 4 people in Lan's family.
2. No, he isn't.
3. He works 5 days in a week.
4. Yes, she is.
5. Her brother is student.



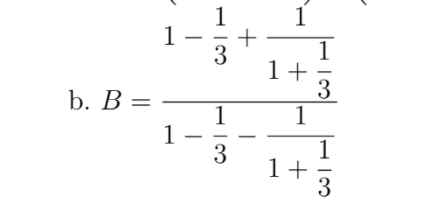 Giúp e vơi ạ!!!
Giúp e vơi ạ!!!


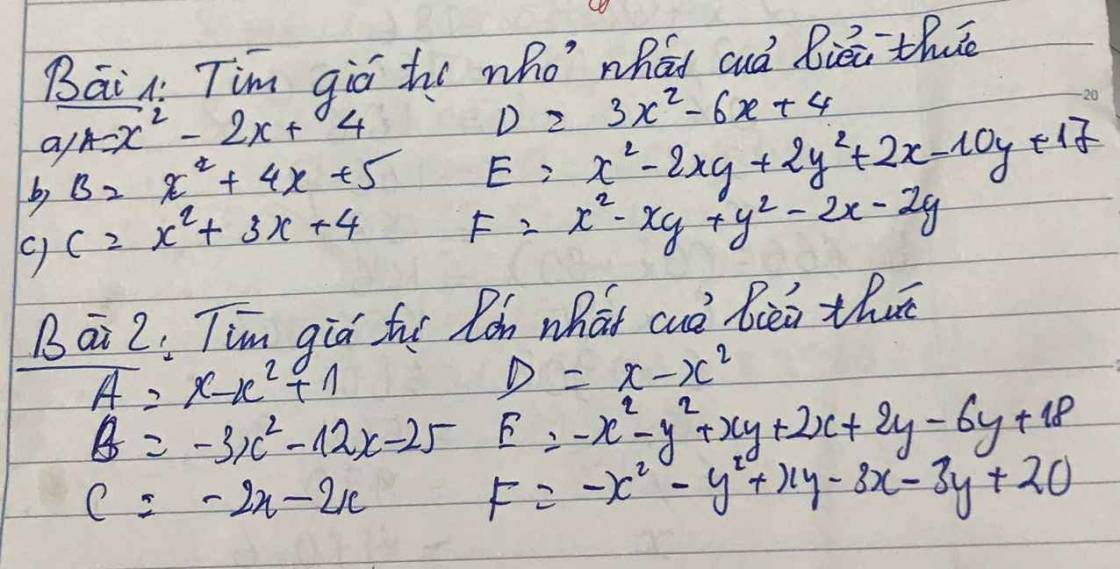

<Bạn tự tóm tắt nha>
Đổi 6m/s=21,6km/h
Vận tốc trung bình của xe là
\(v_{tb}=\dfrac{t\left(\dfrac{3v_1}{4}+\dfrac{1v_2}{4}\right)}{t}=\dfrac{3\cdot21,6}{4}+\dfrac{v_2}{4}\Rightarrow\dfrac{64,8}{4}+\dfrac{v_2}{4}=35\Rightarrow v_2=75,2\left(\dfrac{km}{h}\right)\)
Vậy ...