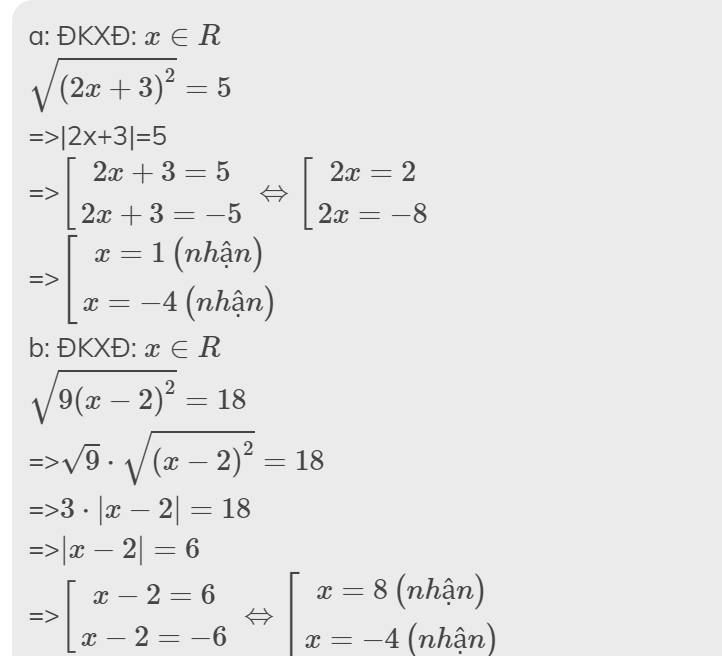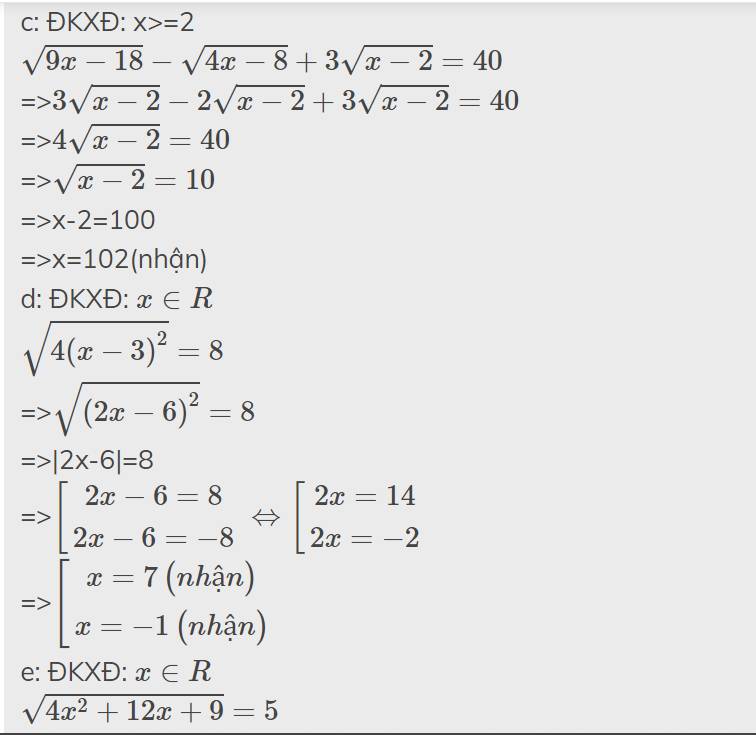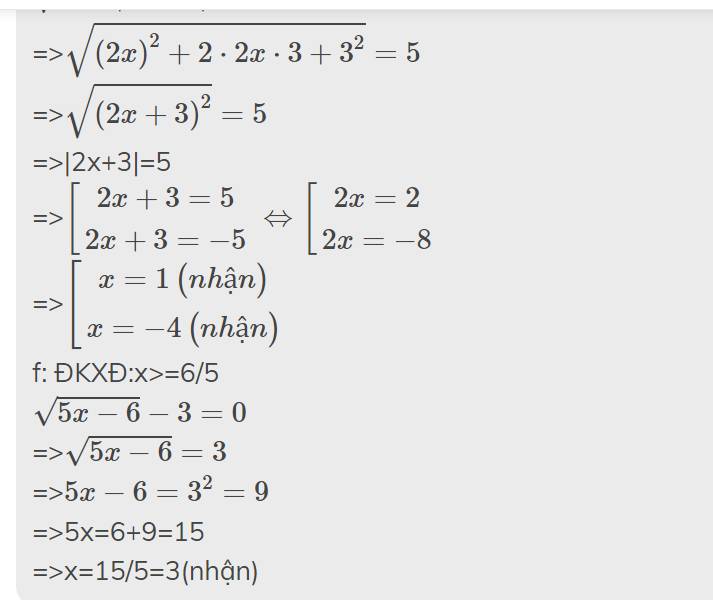giải phương trình \(\sqrt[n]{\left(x-2\right)^2}+4\sqrt[n]{x^2-4}=5\sqrt[n]{\left(x+2\right)^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 9 2017
x=2 không phải là nghiệm nên ta chia cả hai vế của phương trình cho (x-2)2
\(5\sqrt[n]{\left(\frac{x+2}{x-2}\right)^2}-4\sqrt[n]{\frac{x+2}{x-2}}-1=0\)(1)
Đặt\(\sqrt[n]{\frac{x+2}{x-2}}=y\)thì (1)trở thành
\(5y^2-4y-1=0\)
\(\Leftrightarrow\left(y-1\right)\left(5y+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}y_1=1\\y_2=-\frac{1}{5}\end{cases}}\)
Xét \(y=1\Leftrightarrow\sqrt[n]{\frac{x+2}{x-2}}=1\)phương trình vô nghiệm
Xét \(y=-\frac{1}{5}\Leftrightarrow\sqrt[n]{\frac{x+2}{x-2}}=-\frac{1}{5}\)(2)
Nếu n chẵn thì (2) vô nghiệm
Nếu n lẻ thì (2)\(\Leftrightarrow\frac{x+2}{x-2}=-\frac{1}{5^n}\Leftrightarrow x=\frac{2\left(1-5^n\right)}{1+5^n}\)
Tóm lại : Nếu n chẵn thì phương trình đã cho vô nghiệm
Nếu n lẻ thì phương trình có nghiệm \(x=\frac{2\left(1-5^n\right)}{1+5^n}\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 6 2021
a.
Đặt \(\left\{{}\begin{matrix}\sqrt[3]{x+2}=a\\\sqrt[3]{x-2}=b\end{matrix}\right.\) ta được:
\(2a^2-b^2=ab\)
\(\Leftrightarrow\left(a-b\right)\left(2a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\\2a=-b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}a^3=b^3\\8a^3=-b^3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=x-2\left(vô-nghiệm\right)\\8\left(x+2\right)=-\left(x-2\right)\end{matrix}\right.\)
\(\Leftrightarrow x=-\dfrac{14}{9}\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 6 2021
b.
Đặt \(\left\{{}\begin{matrix}\sqrt[3]{65+x}=a\\\sqrt[3]{65-x}=b\end{matrix}\right.\)
\(\Rightarrow a^2+4b^2=5ab\)
\(\Leftrightarrow\left(a-b\right)\left(a-4b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=b\\a=4b\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}a^3=b^3\\a^3=64b^3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}65+x=65-x\\65+x=64\left(65-x\right)\end{matrix}\right.\)
\(\Leftrightarrow...\)
3 tháng 2 2021
Câu 4:
Giả sử điều cần chứng minh là đúng
\(\Rightarrow x=y\), thay vào điều kiện ở đề bài, ta được:
\(\sqrt{x+2014}+\sqrt{2015-x}-\sqrt{2014-x}=\sqrt{x+2014}+\sqrt{2015-x}-\sqrt{2014-x}\) (luôn đúng)
Vậy điều cần chứng minh là đúng
DT
3 tháng 2 2021
2) \(\sqrt{x^2-5x+4}+2\sqrt{x+5}=2\sqrt{x-4}+\sqrt{x^2+4x-5}\)
⇔ \(\sqrt{\left(x-4\right)\left(x-1\right)}-2\sqrt{x-4}+2\sqrt{x+5}-\sqrt{\left(x+5\right)\left(x-1\right)}=0\)
⇔ \(\sqrt{x-4}.\left(\sqrt{x-1}-2\right)-\sqrt{x+5}\left(\sqrt{x-1}-2\right)=0\)
⇔ \(\left(\sqrt{x-4}-\sqrt{x+5}\right)\left(\sqrt{x-1}-2\right)=0\)
⇔ \(\left[{}\begin{matrix}\sqrt{x-4}-\sqrt{x+5}=0\\\sqrt{x-1}-2=0\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}\sqrt{x-4}=\sqrt{x+5}\\\sqrt{x-1}=2\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}x\in\varnothing\\x=5\end{matrix}\right.\)
⇔ x = 5
Vậy S = {5}
BC
0
