Bài 5. Cho hình chữ nhật ABCD, qua A kẻ đường vuông góc với BD tại H. Biết AB = 20 cm , AH = 12 cm a) Tính AD, HD, HB .b) AH cắt CD tại M. Chứng minh: DH.DB=AH.AM C) AH cắt BC tại K. Chứng minh; HA^ 2 =HM.HK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 10 2021
b: Xét ΔBAD vuông tại A có AH là đường cao
nên \(DH\cdot DB=AD^2\left(1\right)\)
Xét ΔADM vuông tại D có DH là đường cao
nên \(AH\cdot AM=AD^2\left(2\right)\)
Từ (1) và (2) suy ra \(DH\cdot DB=AH\cdot AM\)
23 tháng 8 2021
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔADK vuông tại D có DH là đường cao ứng với cạnh huyền AK, ta được:
\(AH\cdot AK=AD^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔADB vuông tại A có AH là đường cao ứng với cạnh huyền BD, ta được:
\(DH\cdot DB=AD^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(AH\cdot AK=DH\cdot DB\)
22 tháng 8 2021
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABD vuông tại A có AH là đường cao ứng với cạnh huyền BD, ta được:
\(DH\cdot DB=AD^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔADK vuông tại D có DH là đường cao ứng với cạnh huyền AK, ta được:
\(AH\cdot AK=AD^2\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(DH\cdot DB=AH\cdot AK\)
20 tháng 10 2021
a) theo đinh lí Py ta go ta có: BD2 = AB2 + AD2 = 62 + 82 => BD = 10
có SABC = 1/2 AD. AB = 1/2 8.6= 24
=> SABC = 1/2 AH. DB => AH = SABC *10 * 1/2 = 4.8
Do mình tính nhẩm nên có sai sót chỗ đáp số nào đó bạn thông cảm cho mình nha
14 tháng 6 2021
a,Vì ABCD là hình chữ nhật => BC = AD = 15 cm
Xét tam giác ABD vuông tại A, đường cao AH
Áp dụng định lí Pytago cho tam giác ABD
\(BD^2=AB^2+AD^2=64+225=289\Rightarrow BD=17\)cm
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AD^2}\Rightarrow\frac{1}{AH^2}=\frac{1}{64}+\frac{1}{225}=\frac{225+64}{64.225}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{289}{14400}\Leftrightarrow AH^2=\frac{14400}{289}\Leftrightarrow AH=\frac{120}{17}\)
14 tháng 6 2021
b, Xét tam giác AHB vuông tại H đường cao HI
\(AH^2=IA.AB\)( hệ thức lượng ) (1)
Xét tam giác ABD vuông tại A đường cao AH
\(AH^2=DH.BH\)( hệ thức lượng ) (2)
Từ (1) ; (2) suy ra \(IA.AB=DH.BH\)( đpcm )
11 tháng 12 2021
\(a,\Delta ABC\) vuông tại A nên \(\widehat{ABC}=90^0-\widehat{ACB}=60^0\)
11 tháng 12 2021
\(b,\left\{{}\begin{matrix}AH\text{ chung}\\\widehat{AHD}=\widehat{AHB}=90^0\\HD=HB\end{matrix}\right.\Rightarrow\Delta AHD=\Delta AHB\left(c.g.c\right)\\ \Rightarrow AD=AB\\ c,DE\text{//}AB\Rightarrow\widehat{HDE}=\widehat{HBA}\left(\text{so le trong}\right)\\ \Rightarrow\widehat{HDE}=\widehat{HDA}\left(\Delta AHD=\Delta AHB\right)\\ \left\{{}\begin{matrix}\widehat{HDE}=\widehat{HBA}\\\widehat{DHE}=\widehat{AHB}\left(\text{đối đỉnh}\right)\\DH=HB\end{matrix}\right.\Rightarrow\Delta BHA=\Delta DHE\left(g.c.g\right)\\ \Rightarrow AB=DE=AD\left(\text{câu b}\right)\\ \left\{{}\begin{matrix}\widehat{HDE}=\widehat{HDA}\\AD=DE\\DH\text{ chung}\end{matrix}\right.\Rightarrow\Delta DHA=\Delta DHE\left(g.c.g\right)\)
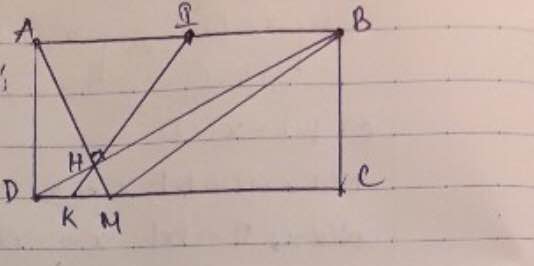
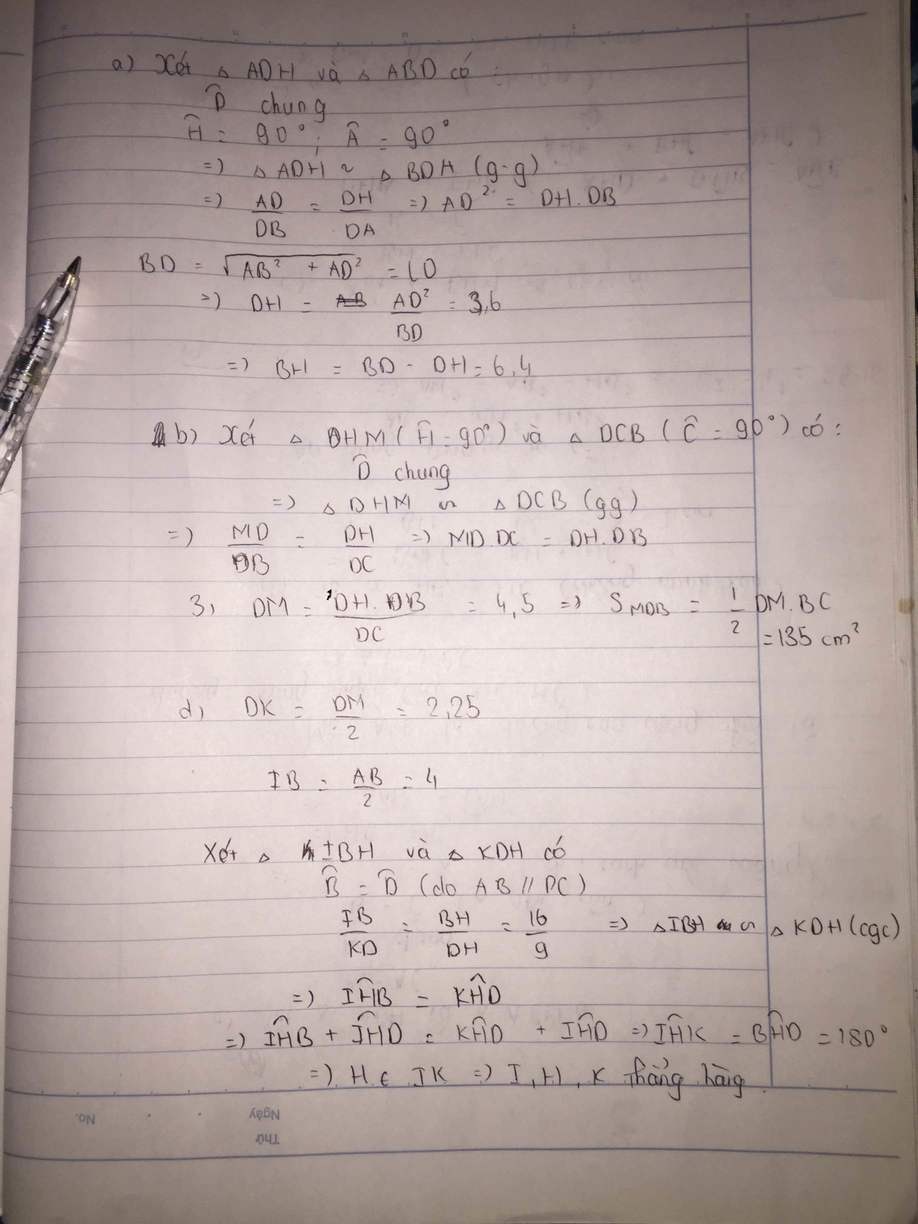
b: Xét ΔADM vuông tại D có DH là đường cao ứng với cạnh huyền AM
nên \(AH\cdot AM=AD^2\left(1\right)\)
Xét ΔADB vuông tại A có AH là đường cao ứng với cạnh huyền DB
nên \(DH\cdot DB=AD^2\left(2\right)\)
Từ (1) và (2) suy ra \(DH\cdot DB=AH\cdot AM\)