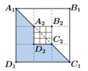
Nếu cách chia hình vuông thành 16 hình vuông nhỏ . Lần lượt tô màu như sau : Tô màu vàng 3 phần 16 hình vuông , tô màu cam một phần tư hình vuông , tô màu xanh một phần 8 hình vuông , tô màu tím 5 phần 16 hình vuông . số ô vuông chưa tô màu chiếm bao nhiêu phần hình vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 2 2017
Gọi diện tích được tô màu ở mỗi bước là 
Dễ thấy dãy các giá trị
u
n
là một cấp số nhân với số hạng đầu
u
1
=
4
9
và công bội q =
1
9
Gọi
S
k
là tổng của k số hạng đầu trong cấp số nhân đang xét thì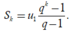 
Để tổng diện tích phần được tô màu chiếm 49,99% khi và chỉ khi
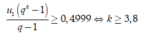
Vậy cần ít nhất 4 bước. Chọn B.
3 tháng 3 2023
Hình vuông có 3 cách tô
Hiình tròn có 2 cách tô
=> 3x2=6 cách tô
18 tháng 5 2023
Hình vuông có 3 cách tô
Hiình tròn có 2 cách tô
=> 3x2=6 cách tô
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Diện tích ô vuông màu xanh sau lần phân chia thứ nhất là \(\frac{1}{9}\), số ô vuông màu xanh được tạo thêm là \({8^0}\).
Diện tích ô vuông màu xanh sau lần phân chia thứ hai là \(\frac{1}{{{9^2}}}\), số ô vuông màu xanh được tạo thêm là \({8^1}\).
Diện tích ô vuông màu xanh sau lần phân chia thứ ba là \(\frac{1}{{{9^3}}}\), số ô vuông màu xanh được tạo thêm là \({8^2}\).
Diện tích ô vuông màu xanh sau lần phân chia thứ tư là \(\frac{1}{{{9^4}}}\), số ô vuông màu xanh được tạo thêm là \({8^3}\).
Diện tích ô vuông màu xanh sau lần phân chia thứ ba là \(\frac{1}{{{9^5}}}\), số ô vuông màu xanh được tạo thêm là \({8^4}\).
Tổng diện tích các ô vuông màu xanh là
\(\frac{1}{9} + \frac{1}{{{9^2}}} \times {8^1} + \frac{1}{{{9^3}}} \times {8^2} + \frac{1}{{{9^4}}} \times {8^3} + \frac{1}{{{9^5}}} \times {8^4} = 0,445\).
27 tháng 1 2019
An vẽ hai hình vuông bằng nhau. An chia hình vuông thứ nhất thành 4 phần bằng nhau rồi An tô màu 3 phần. An chia hình vuông thứ hai thành 12 phần bằng nhau. Hỏi An phải tô màu mấy phần ở hình thứ hai để diện tích phần đã tô màu ở hai hình bằng nhau? An cần tô 9 phần.