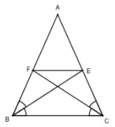
Cho tam giác ABC cân tại A, các tia phân giác BE, CF. Chứng minh BFEC là hình thang cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 9 2021
\(a,\left\{{}\begin{matrix}\widehat{B_1}=\widehat{B_2}=\dfrac{1}{2}\widehat{ABC};\widehat{C_1}=\widehat{C_2}=\dfrac{1}{2}\widehat{ACB}\\\widehat{ABC}=\widehat{ACB}\left(\Delta ABC.cân.tại.A\right)\end{matrix}\right.\Rightarrow\widehat{B_1}=\widehat{B_2}=\widehat{C_1}=\widehat{C_2}\\ \left\{{}\begin{matrix}\widehat{B_1}=\widehat{C_1}\\AB=AC\\\widehat{A}\end{matrix}\right.\Rightarrow\Delta AEB=\Delta AFC\left(g.c.g\right)\Rightarrow AE=AF\\ \Rightarrow\Delta AEF.cân\)
\(b,\left\{{}\begin{matrix}AE=AF\\AB=AC\end{matrix}\right.\Rightarrow AB-AF=AC-AE\Rightarrow BF=CE\\ \left\{{}\begin{matrix}BF=CE\\\widehat{ABC}=\widehat{ACB}\\BC.chung\end{matrix}\right.\Rightarrow\Delta BFC=\Delta CEB\left(c.g.c\right)\)
\(c,\widehat{AFE}=\dfrac{180^0-\widehat{A}}{2}\left(\Delta AEF.cân\right);\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\left(\Delta ABC.cân\right)\\ \Rightarrow\widehat{AFE}=\widehat{ABC}\)
Mà 2 góc này ở vị trí đồng vị nên \(EF//BC\Rightarrow BFCE\) là hthang
Mà \(\widehat{ABC}=\widehat{ACB}\) nên BFCE là hthang cân
CM
11 tháng 9 2018
+) Do BE và CF lần lượt là tia phân giác của góc B và góc C nên ta có:
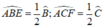
Mà tam giác ABC cân tại A nên ∠ B = ∠ C
Suy ra: ∠ ABE = ∠ ACF
Xét hai tam giác AEB và AFC
Có AB = AC ( ∆ ABC cân tại A)
∠ ABE = ∠ ACF (chứng minh trên)
∠ A là góc chung
⇒ ∆ AEB = ∆ AFC (g.c.g) ⇒ AE = AF ⇒ ∆ AEF cân tại A
⇒ ∠ AFE = ( 180 0 − ∠ A) / 2 và trong tam giác ∆ ABC: ∠ B = ( 180 0 − ∠A) / 2
⇒ ∠ AFE = ∠ B ⇒ FE//BC ( có hai góc ở vị trí đồng vị bằng nhau).
⇒ Tứ giác BFEC là hình thang.
Vì FE//BC nên ta có: ∠ FEB = ∠ EBC (so le trong)
Lại có: ∠ FBE = ∠ EBC ( vì BE là tia phân giác của góc B)
⇒ ∠ FBE = ∠ FEB
⇒ ∆ FBE cân ở F ⇒ FB = FE
⇒ Hình thang BFEC là hình thang cân có đáy nhỏ bằng cạnh bên (đpcm)
14 tháng 8 2017
A B C E F
Ta có: \(\Delta ABC\) cân tại A (gt)
mà BE, CF lần lượt là tia phân giác của \(\widehat{ABC}\) và \(\widehat{ACB}\) (gt)
=> BE = CF
Xét \(\Delta ABE\) và \(\Delta ACF\) có:
BE = CF (cmt)
\(\widehat{ABE}=\widehat{ACF}\) \(\left(\widehat{ABC}=\widehat{ACB}=2\widehat{ABE}=2\widehat{ACF}\right)\)
AB = AC (\(\Delta ABC\) cân tại A)
Do đó: \(\Delta ABE=\Delta ACF\left(c.g.c\right)\)
=> AE = AF (2 cạnh tương ứng)
=> \(\Delta AFE\) cân tại A
mà \(\Delta ABC\) cân tại A
nên \(\widehat{ABC}=\widehat{AFE}\)
mà chúng ở vị trí đồng vị
=> FE // BC (dấu hiệu nhận biết)
=> BFEC là hình thang
mà BE = CF
=> BFEC là hình thang cân
Ta có: EF // BC (cmt)
=> \(\widehat{EFC}=\widehat{FCB}\) (2 góc so le trong)
mà \(\widehat{FCB}=\widehat{ECF}\) (CF là tia phân giác \(\widehat{ECB}\))
=> \(\Delta FEC\) cân tại E (t/c tam giác cân)
=> FE = EC (Đ/N tam giác cân)
mà hình thang BFEC cân
=> BFEC là hình thang cân có đáy nhỏ bằng cạnh bên
31 tháng 8 2019
góc A là góc chung
AB=AC(giả thiết)
góc ABE= góc ACF(cmt)
=>tam giác ABE= tam giác ACF(c.g.c)
=>AE=AF
=>tam giác AEF cân tại A
=>AEF=180-A/2 (1)
có tam giác AEF cân tại A (gt) 180 độ nhé
=>góc ABC=180-A/2 (2)
từ (1) và (2) nên ^AFE=^ABC 2 góc đòng vị
=>FE song song với BC
mà ^B=^C
=>tứ giác BFEC là ht cân
CT
24 tháng 9 2021
a) Ta có tam giác ABC cân tại A
=> góc B= góc C
=> 1/2 góc C= 1/2 góc B
=> ABE=ACF
Xét tam giác ABE và tam giác AFC có:
AB=AC(gt)
A(chung)
ABE=ACF(cmt)
=> tam giac ABE= tam giác ACF(g.c.g)
=> AF=AE
=> tam giác AEF cân tại A
b)Ta có góc B= góc C
=> 1/2 góc B=1/2 góc C=>EBC=FCB
Theo câu a, ta có tam giác ABE= tam giác ACF(g.c.g)
=> BE=CF
Xét tam giác BFC vá tam giác CEB có
BE=CF(tam giác ABE= tam giác ACF)
FCB=ECB(cmt)
BC(chung)
=> tam giác BFC= tam giác CEB(c.g.c0
c) Tam giác AFE cân tại A
=>góc AFE=(180*-A)/2
Tam giác ABC cân tại B=>ABC=(180*-A)/2
=> ABC=AFE
=> FE//BC(1)
Ta có: FB=AB-AF
EC=AC-AE
AB=AC
AF=AE
=> FB=EC(2)
Từ (1)(2)=> tứ giác BFEC là hình thang cân
Xét ΔABE và ΔACF có:
^A : góc chung
AB=AC(gt)
^ABE=^ACF(cmt)
=>ΔABE=ΔACF(g..c.g)
=> AE=AF
=>ΔAEF cân tại A
=> AFEˆ=180−Aˆ2AFE^=180−A^2 (1)
Có: ΔABC cân tại A(gt)
=> ABCˆ=180−Aˆ2ABC^=180−A^2 (2)
Từ (1)(2) suy ra:
^AFE=^ABC. MÀ hai góc mày ở vị trí đồng vị
=>FE//BC
Mà ^B=^C(gt)
=> tứ giác BFEC là ht cân