Tính diện tích của một tam giác cân có cạnh đáy bằng a và cạnh bên bằng b.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

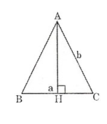
Gọi h là chiều cao của tam giác cân.
Theo định lí Pitago ta có:
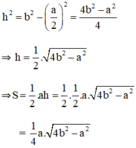

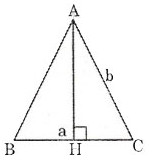
Xét Δ ABC cân tại A có AB = AC = b, BC = a.
Từ A kẻ AH ⊥ BC.
Ta có BH = HC = 1/2BC = a/2
Khi đó ta có: S A B C = 1 2 A H . B C = 1 2 . a . A H
Áp dụng định lý Py – to – go ta có:
A C 2 = A H 2 + H C 2 ⇒ A H = A C 2 - H C 2
Khi đó SABC = 1/2AH.BC
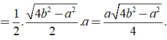
Do đó diện tích của tam giác đều các cạnh bằng a là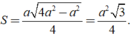

Xét Δ ABC cân tại A có AB = AC = b, BC = a.
Từ A kẻ AH ⊥ BC.
Ta có BH = HC = 1/2BC = a/2
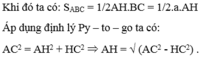
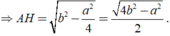
Khi đó SABC = 1/2AH.BC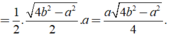
Do đó diện tích của tam giác đều các cạnh bằng a là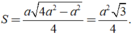

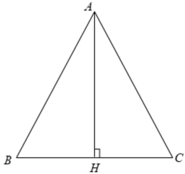
Gọi h là chiều cao của tam giác cân có đáy là a và cạnh bên là b.
Theo định lý Pitago ta có
h2 = b2 -  =
= 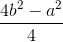
h = 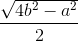
Nên S =  ah =
ah =  a.
a. 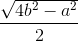 =
=  a.
a. 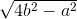 .
.

Câu 1:
Diện tích tam giác đều cạnh 3cm là:
\(S=\dfrac{3^2\cdot\sqrt{3}}{4}=\dfrac{9\sqrt{3}}{4}\left(cm^2\right)\)
Câu 2:
Nửa chu vi tam giác là:
\(P=\dfrac{C}{2}=\dfrac{8+8+6}{2}=\dfrac{22}{2}=11\left(cm\right)\)
Diện tích tam giác là:
\(S=\sqrt{P\cdot\left(P-A\right)\cdot\left(P-B\right)\cdot\left(P-C\right)}=\sqrt{11\cdot\left(11-8\right)^2\cdot\left(11-6\right)}\)
\(=\sqrt{11\cdot5\cdot9}=3\sqrt{55}\left(cm^2\right)\)
Gọi h là chiều cao của tam giác cân có đáy là a và cạnh bên là b.
Theo định lý Pitago ta có
h2 = b2 – =
= 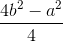
h =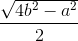
Nên S = ah =
ah =  a.
a. 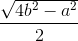 =
=  a.
a. 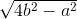
Tự vẽ hình nhé bạn
Gọi h là chiều cao của tam giác cân có đáy là a và cạnh bên là b.
Theo định lý Pitago ta có :
\(h^2=b^2-\left(\frac{a}{b}\right)^2=\frac{4b^2-a^2}{4}\)
\(h=\frac{\sqrt{4b^2-a^2}}{2}\)
\(\Rightarrow S=\frac{1}{2}ah=\frac{1}{2}a.\frac{\sqrt{4b^2-a^2}}{2}=\frac{1}{4}a.\sqrt{4b^2-a^2}\)