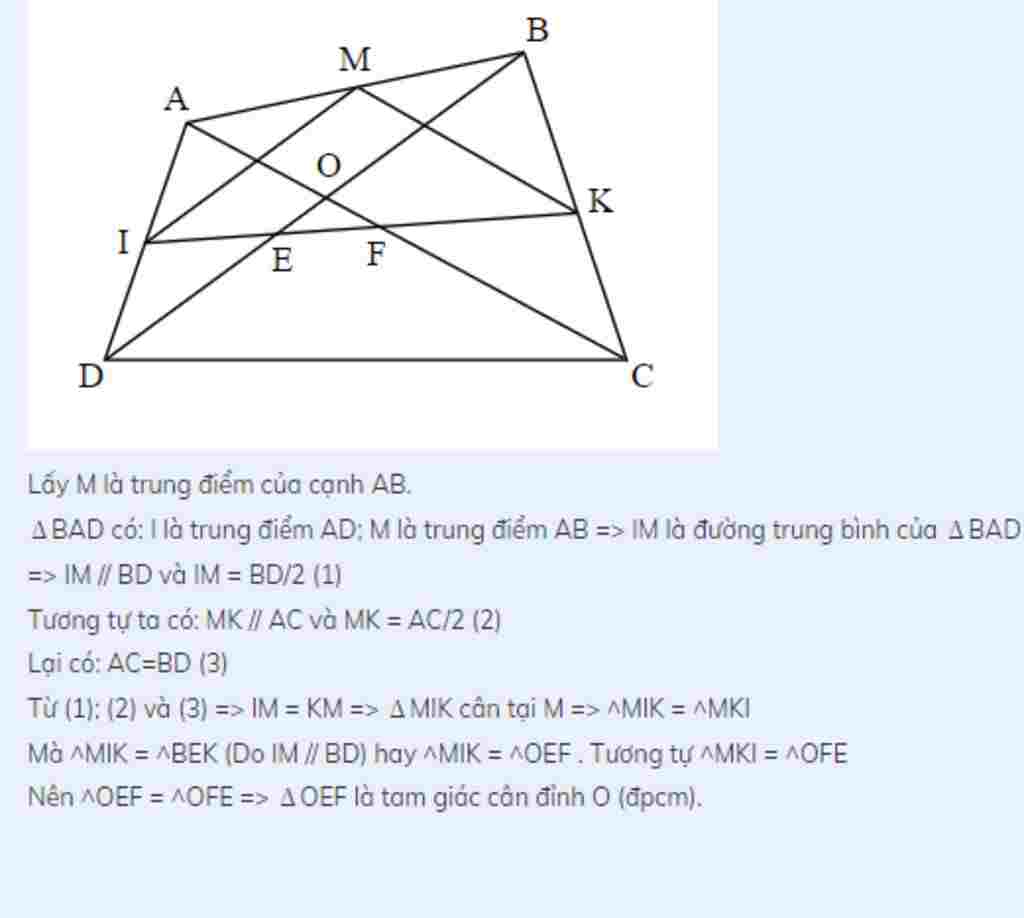
Cho tứ giác ABCD có 2đường chéo cắt nhau tại O. I và K theo thứ tự là trung điểm của AD và BC. Đường thẳng I,K cắt BC,AD theo thứ tự ở E,F. Chứng minh OEF là tam giác cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

1 tháng 9 2017
Đây là hình của bài
nhưng mik ko chắc đúng
vì mik mới học lớp 7
thông cảm nha

26 tháng 8 2018
Lấy M là trung điểm của cạnh AB.
\(\Delta\)BAD có: I là trung điểm AD; M là trung điểm AB => IM là đường trung bình của \(\Delta\)BAD
=> IM // BD và IM = BD/2 (1)
Tương tự ta có: MK // AC và MK = AC/2 (2)
Lại có: AC=BD (3)
Từ (1); (2) và (3) => IM = KM => \(\Delta\)MIK cân tại M => ^MIK = ^MKI
Mà ^MIK = ^BEK (Do IM // BD) hay ^MIK = ^OEF . Tương tự ^MKI = ^OFE
Nên ^OEF = ^OFE => \(\Delta\)OEF là tam giác cân đỉnh O (đpcm).