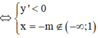**Cần gấp ạ cảm ơn!<3
Tìm tất cả số nguyên m sao cho hàm số f(x) = mx +√m+5m+5 nghịch biến trên R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
UN
0
AH
Akai Haruma
Giáo viên
14 tháng 10 2021
Lời giải:
ĐK: $m\geq -5$
Để hàm nghịch biến trên $R$ thì $m<0$
Vậy $-5\leq m< 0$. Vì $m$ nguyên nên $m\in\left\{-5;-4;-3;-2;-1\right\}$
TB
1
1 tháng 11 2021
Để hàm số này nghịch biến thì \(\left\{{}\begin{matrix}a< 0\\a+5\ge0\end{matrix}\right.\Leftrightarrow-5\le a< 0\)
TB
1
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
Hàm nghịch biến trên R khi:
\(\left\{{}\begin{matrix}a< 0\\a+5\ge0\end{matrix}\right.\) \(\Rightarrow-5\le a< 0\)
CM
5 tháng 12 2019
Đáp án D
Ta có y ' = cos x − m .
Hàm số nghịch biến trên R
⇔ y ' ≤ 0 , ∀ x ∈ ℝ ⇒ cos x − m ≤ 0 ∀ x ∈ ℝ ⇔ cos x ≤ m ∀ x ∈ ℝ ⇒ m ≥ M a x ℝ cos x = 1.
CM
17 tháng 5 2018
Đáp án D
Phương pháp giải:
Dựa vào điều kiện để hàm số b1 trên b1 đồng biến hoặc nghịch biến trên khoảng
Lời giải: Ta có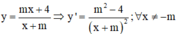 
Yêu cầu bài toán 
