Cho ba số phân biệt 12; 56; ab
-Ghép liên tiếp hai trong ba số trên để được những số có 4 chữ số, hãy viết những số đó
-Tìm ab biết trung bình cộng của các số có 4 chữ số vừa tạo thành bằng 3434
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp:
+) Tìm điều kiện để phương trình y’ = 0 có hai nghiệm phân biệt thỏa mãn ĐKXĐ.
+) Viết phương trình đường thẳng AB. Để A, B, C thẳng hàng ó C ∈ AB
Cách giải: TXĐ: D = R\{|m|}
Ta có:
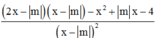
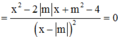
![]()
<=> 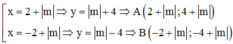
=> Đồ thị hàm số luôn có hai điểm cực trị A, B phân biệt.
Đường thẳng AB có phương trình:
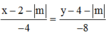
![]()
![]()
Để A, B, C(4;2) phân biệt thẳng hàng ó CAB => 2 = 4.2 - |m| ó |m| = 6
Khi đó ta có: B(4;2) ≡ C => không thỏa mãn.
Vậy không có giá trị nào của m thỏa mãn yêu cầu bài toán

Đáp án A.
Diện tích tam giác đều cạnh a là S a 2 3 4 .
Vậy thể tích khối lăng trụ cần tính là V = S . h = a . a 2 3 4 = a 3 3 4 .

Khi 3 đường thẳng đôi một song song thì số đường tròn tiếp xúc với cả 3 đường thẳng trên là 0.
Khi có 2 đường thẳng song song và cắt đường tròn thì số đường tròn tiếp xúc với cả 3 đường thẳng trên là 2.
Khi 3 đường thẳng đôi một cắt nhau thì số đường tròn tiếp xúc với cả 3 đường thẳng trên là 4.
ĐÁP ÁN B

Đáp án C
Nếu ba đường thẳng a,b,c đôi một cắt nhau và không đồng phẳng thì chúng chỉ có thể đồng quy tại một điểm.

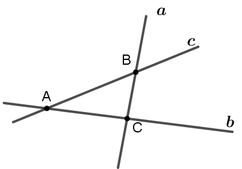

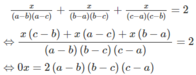
Do a, b, c đôi một khác nhau nên 2(a - b)(b - c)(c - a) ≠ 0. Vậy phương trình đã cho vô nghiệm.

1/3 = 2/6 = 4/12 = 8/24
36/96 = 18/48 = 9/24 = 3/8
12/18 = 6/9 = 2/3 = 24/36
Theo đề bài
\(\frac{\left(1256+5612+\overline{12ab}+\overline{ab12}+\overline{56ab}+\overline{ab56}\right)}{6}=3434\)
\(\frac{1256+5612+1200+\overline{ab}+100x\overline{ab}+12+5600+\overline{ab}+100x\overline{ab}+56}{6}=3434\)
\(202x\overline{ab}+13736=6x3434\)
\(202x\overline{ab}=6868\Rightarrow\overline{ab}=6868:202=34\)