A= 17,58 nhân 43 + 57 nhân 17,58
trên
293 nhân a
a, tính giá trị biểu thức a=2
b, tính a để A=2
c, tìm số tự nhiên a để A có giá trị lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 8 2018
A=\(\frac{17,58.43+57.17,58}{293.a}\)
a) \(a=2\)
\(\Rightarrow A=\frac{17,58.\left(43+57\right)}{293.2}\)
\(\Rightarrow A=\frac{17,58.100}{586}\)
\(\Rightarrow A=\frac{1758}{586}=3\)
b)\(A=2\)
\(\Rightarrow\frac{1758}{293.a}=2\)
\(\Leftrightarrow1758:2=293.a\)
\(\Leftrightarrow879=293.a\)
\(\Rightarrow a=879:293=3\)
c) Để A có GTLN
\(\Rightarrow293.a\)có giá trị nhỏ nhất
Mà :\(a>0\)( Vì :\(293.a\ne0\))
Mà :\(1758:293=6\)
\(\Rightarrow GTLN\)\(A=6\)\(Khi:293.a=293\)
\(\Rightarrow a=1\)
TN
19 tháng 8 2018
a/ A=\(\frac{17,58.\left(43+57\right).17,58}{293.a}\)
với \(a=2\)ta có
A = \(\frac{17,58.100.17,58}{293.2}\)
\(=\frac{30905,64}{586}\)
\(=\frac{2637}{50}\)
b/ để A = 2
<=> \(\frac{17,58\left(43+57\right).17,58}{293.a}\)\(=2\)
<=> \(1758.17,58=586a\)
<=> \(a=\frac{2637}{50}\)
học tốt
22 tháng 7 2018
\(B=\frac{17,58\left(43+57\right)}{293.a}=\frac{1758}{293.a}\)
a) Ta có \(B=\frac{1758}{293.a}=2\)
<=> \(293.a.2=1758\)
<=> 586.a=1758
<=> a=3
b)Để Bmax thì 293.a bé nhất và dương
=> 293.a=293
=> a=1
lúc đó \(B=\frac{1758}{293}=6\)
Vậy Bmax=6 <=> a=1
CM
6 tháng 6 2019
a, 17,58 x 43 + 57 x 17,58
= 17,58 x 43 + 17,58 x 57 (tính giao hoán)
= 17,58 x (43 + 57) = 17,58 x 100 = 1758 (nhân 1 số với 1 tổng)
b, 43,57 x 2,6 x (630 – 315 x 2)
= 43,57 x 2,6 x (630 – 630)
= 43,57 x 2,6 x 0 = 0
PT
1
CM
22 tháng 11 2019
17,58 x 43 + 57 x 17,58
= 17,58 x 43 + 17,58 x 57 (tính giao hoán)
= 17,58 x (43 + 57) = 17,58 x 100 = 1758 (nhân 1 số với 1 tổng)
CM
26 tháng 3 2017
a, 17,58 x 43 + 57 x 17,58
= 17,58 x 43 + 17,58 x 57 (tính giao hoán)
= 17,58 x (43 + 57) = 17,58 x 100 = 1758 (nhân 1 số với 1 tổng)
b, 43,57 x 2,6 x (630 – 315 x 2)
= 43,57 x 2,6 x (630 – 630)
= 43,57 x 2,6 x 0 = 0
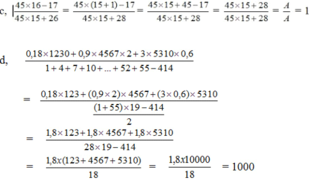
ở số chia, từ 1 tới 55 là các số mà 2 số liên tiếp hơn kém nhau 3 đơn vị nên từ 1 đến 55 có (55 – 1) :3 + 1 = 19 số).
e, 9,8 + 8,7 + 7,6 + . . . + 2,1 – 1,2 – 2,3 – 3,4 - . . . – 8,9
= (9,8 – 8,9) + (8,7 – 7,8) + . . . +(2,1 – 1,2)
= 0,9 + 0,9 + 0,9 + 0,9 + 0,9
= 0,9 x 5 = 4,5.
giải :
a,\(A=\frac{17,58\cdot\left(43+57\right)}{293\cdot2}\)=\(\frac{17,58.100}{586}\)=\(\frac{1758}{586}=3\)
b,\(\frac{17,58.\left(43+57\right)}{293.a}\)= 2 (=)\(\frac{17,58.100}{293\cdot a}\)=2 (=) \(\frac{1758}{293.a}=2\)(=)293.a.2=1758(=)586.a=1758(=)a=3
c,tương tự ý b ra : \(\frac{1758}{293\cdot a}\)để A lớn nhất => 293.a phải là số nguyên dương nhỏ nhất=>293.a=1(=)a=\(\frac{1}{293}\)