Giúp mình với.
Cảm ơn ạ
Bài 1- Một vật chuyển động thẳng theo phương trình x=4t^2 + 20t (cm/s)
1.Tính quãng đường chuyển động của vật đi đc từ t1=2s đến t2=5s.Suy ra vận tốc trung bình trong khoảng thời gian này.
2.Tính vận tốc lúc t=3s
Bài2 Một vật chuyển động với phương trình x=10-20t-2t*2 (m)
a.Xác định a,toạ độ và vận tốc ban đầu
b.vận tốc ở thời điểm t=3s
c.vận tốc lúc vật có toạ độ x=0
d.toạ độ lúc vận tốc là V=-40m/s
e.Quãng đường đi từ t=2s đến t=10s
g.Quãng đường đi được khi vận tốc thay đổi từ V1=-30m/s đến V2=-40m/s


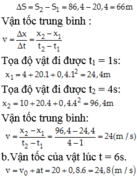



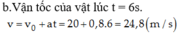


Bài 1:
Giải:
1. Quãng đường vật đi được trong giây thứ nhất là:
\(s_1=x_1=4.t_1'^2+20t_1'=4.1^2+20.1=24\left(cm\right)\)
Quãng đường vật đi được từ khi xuất phát đến giây thứ 5 là:
\(s_5=x_5=4.t_5^2+20t_5=4.5^2+20.5=200\left(cm\right)\)
Quãng đường vật đi được từ giây thứ 2 đến giây thứ 5 là:
\(s_{2\rightarrow5}=s_5-s_1=200-24=176\left(cm\right)\)
Vận tốc trung bình trong khoảng thời gian này là:
\(v_{tb}=\dfrac{s_{2\rightarrow5}}{\Delta t}=\dfrac{176}{t_2-t_1}=\dfrac{176}{5-2}\approx58,67\left(cm/s\right)\)
2. Theo phương trình chuyển động: \(x=4t^2+20t\)
Ta có: \(v_0=20cm/s\\ a=4cm/s^2\)
Vận tốc lúc t=3s là:
\(v=v_0+a.t=20+4.3=32\left(cm/s\right)\)
Vậy:....
BÀI 1 :
Quãng đường vật đi trong 2s,5s là:s2=4 . \(2^2\) + 20 . 2 = 56 m
s5=4.\(5^2\)+20.5=200m
Quãng đường vật đi từ 2s đến 5s là:
s=s5−s2=144m
Vận tốc tb trong thời gian ấy là:
\(v_{tb}\)=S/t=144/3=48m/s
Vận tốc lúc t=3s là:
\(v_3\)=\(v_0\)+at=20+8.3=44m/s