bài 6 (SGK_trang109) lớp 7 toán hình tam giác
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 1 2019
Bai 1: Cho tam giac ABC vuong tai A. Tia phan giac cua goc B cat AC o D. Ke DE vuong goc voi BC .CMR: AB bang BE
Bai 2: Cho tam giac ABC, D la trung diem cua AB. Duong thang qua D va song2 voi BC cat AC o E, duong thang qua E va song2 voi AB cat BC o F.CMR:
a, AD bang EF
b, \(\Delta ADE=\Delta EFC\)
c,\(AE=EC\)
Bai 3:* Cho tam giac ABC ,D la trung diem cua AB ,E la trung diem cua AC .Ve diem F : E la trung diem cua DF.CMR:
a,\(DB=CF\)
b,\(\Delta BDC=\Delta FCD\)
c,\(DE//BC,DE=\frac{1}{2}BC\)
HTDT
Q
16 tháng 1 2023
Lời giải
a) Diện tích hình chữ nhật ABCD gồm:
8 × 4 = 32 (ô vuông)
Diện tích hình tam giác MDC gồm 12 ô vuông và 8 nửa ô vuông (4 ô vuông), tức là gồm:
12 + 4 = 16 (ô vuông)
Diện tích hình chữ nhật ABCD gấp diện tích hình tam giác MDC số lần là:
32 : 16 = 2 (lần)
b) Diện tích hình chữ nhật IKCD gồm:
8 × 2 = 16 (ô vuông)
Diện tích hình chữ nhật IKCD bằng diện tích hình tam giác MDC.
Nhớ tick mình nhé, chúc bạn học tốt!
VN
16 tháng 9 2017
Tự vẽ hình nha
Diện tích hình tam giác là:
360 :3 x2 =240(cm2)
đáp số:240 cm2
5 tháng 9 2016
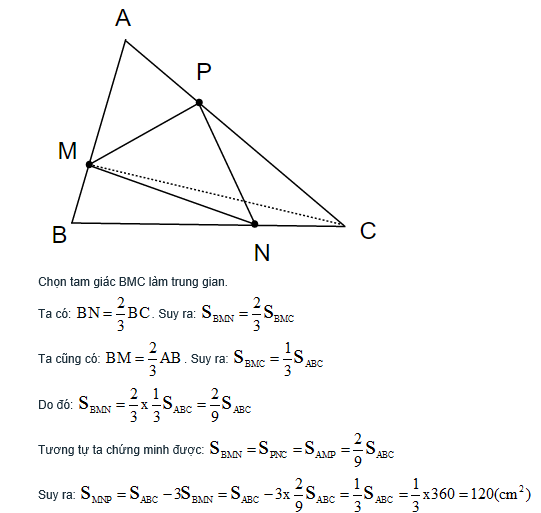
A B C M N P
Nối MC,BP.Từ giả thiết,ta có AM = 2/3 AB ; MB = 1/3 AB ; CP = 2/3 AC ; AP = 1/3 AC ; BN = 2/3 BC ; CN = 1/3 BC
SAPB = 1/3 SABC (vì chung đường cao hạ từ P và có đáy AP = 1/3 AC)
SAPM = 2/3 SAPB = 2/3.1/3 SABC = 2/9 SABC (____________________ P ________ AM = 2/3 AP)
SBMC = 1/3 SABC (____________________ C ________ BM = 1/3 AB)
SBMN = 2/3 SBMC = 2/3.1/3 SABC = 2/9 SABC (____________________ M ________ BN = 2/3 BC)
SBCP = 2/3 SABC (____________________ B ________ CP = 2/3 AC)
SCNP = 1/3 SBCP = 2/3.1/3 SABC = 2/9 SABC (____________________ P ________ CN = 1/3 BC)
=> SMNP = SABC - SAPM - SBMN - SCNP = SABC - 2/9 SABC - 2/9 SABC - 2/9 SABC = 1/3 SABC = 1/3.360 = 120 (cm2)
NY
27 tháng 12 2019
https://taimienphi.vn/download-70-bai-tap-toan-nang-cao-lop-7-37125
link này
#Châu's ngốc
dai qua
Xét ΔAHI có ˆH=900ΔAHI có H^=900 ta có:
ˆA+ˆAIH=900A^+AIH^=900 (1) (tổng hai góc nhọn của tam giác vuông phụ nhau)
Xét ΔBKI có ˆK=900ΔBKI có K^=900 ta có:
ˆB+ˆBIK=900B^+BIK^=900 (2) (tổng hai góc nhọn của tam giác vuông phụ nhau)
Từ (1) và (2) suy ra: ˆA+ˆAIH=ˆB+ˆBIKA^+AIH^=B^+BIK^
Mà ˆAIH=ˆBIKAIH^=BIK^ (hai góc đối đỉnh)
Nên suy ra ˆB=ˆA=400B^=A^=400
Vậy ˆB=x=400B^=x=400
Hình 56)
Xét ΔABD có ˆADB=900ΔABD có ADB^=900 ta có:
ˆABD+ˆA=900ABD^+A^=900 (4) (tổng hai góc nhọn của tam giác vuông phụ nhau)
Xét ΔACE có ˆAEC=900ΔACE có AEC^=900 ta có:
ˆACE+ˆA=900ACE^+A^=900 (5) (tổng hai góc nhọn của tam giác vuông phụ nhau)
Từ (4) và (5) suy ra ˆACE=ˆABD=250ACE^=ABD^=250
Vậy x=250x=250
Hình 57)
Ta có: ˆNMP=ˆNMI+ˆPMI=900NMP^=NMI^+PMI^=900 (6)
Xét ΔMNI có ˆMIN=900ΔMNI có MIN^=900 ta có :
ˆN+ˆNMI=900N^+NMI^=900 (7) (tổng hai góc nhọn của tam giác vuông phụ nhau)
Từ (6) và (7) suy ra ˆN=ˆPMI=600N^=PMI^=600
Vậy x=600x=600
Hình 58)
Xét ΔAHE có ˆAHE=900ΔAHE có AHE^=900 ta có :
ˆE+ˆA=900E^+A^=900 (tổng hai góc nhọn của tam giác vuông phụ nhau)
ˆE=900−ˆA=900−550=350E^=900−A^=900−550=350
Vì ˆKBHKBH^ là góc ngoài tại đỉnh BB của tam giác BKEBKE nên
ˆKBH=ˆBKE+ˆEKBH^=BKE^+E^=900+350=1250=900+350=1250
Vậy x=1250