Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta chứng minh được AEDF là hình bình hành Þ AD Ç È = I. I là trung điểm của AD và EF. Suy ra E đối xứng với F qua I
a: Xét tứ giác AKMN có
MN//AK
AN//MK
Do đó: AKMN là hình bình hành
mà \(\widehat{NAK}=90^0\)
nên AKMN là hình chữ nhật
b: Xét ΔAMQ có
AN là đường cao
AN là đường trung tuyến
Do đó: ΔAMQ cân tại A
mà AN là đường cao
nên AN là tia phân giác của góc MAQ(1)
Xét ΔAME có
AK là đường cao
AK là đường trung tuyến
DO đó: ΔAME cân tại A
mà AK là đường cao
nên AK là tia phân giác của góc MAE(2)
Từ (1) và (2) suy ra \(\widehat{QAE}=2\cdot\left(\widehat{MAN}+\widehat{MAK}\right)=2\cdot90^0=180^0\)
hay Q,E,A thẳng hàng
a) IM // AC, AB \(\perp AC\)
\(\Rightarrow\)IM \(\perp AB\) \(\Rightarrow\)\(\widehat{AMI}=90^0\)
IN // AB, AB \(\perp AC\)
\(\Rightarrow\)IN \(\perp AC\) \(\Rightarrow\)\(\widehat{ANI}=90^0\)
Tứ giác AMIN có: \(\widehat{AMI}=\widehat{MAN}=\widehat{ANI}=90^0\)
nên AMIN là hình chữ nhật
b) Hình chữ nhật AMIN là hình vuông
\(\Leftrightarrow\)AI là phân giác \(\widehat{BAC}\)
mà AI đồng thời la trung tuyến của \(\Delta ABC\)
\(\Rightarrow\)\(\Delta ABC\)vuông cân tại A
a: Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
b: Vì ABCD là hình bình hành
nên AC và BD cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của BD
hay B và D đối xứng nhau qua O
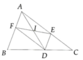
a) (mình nghĩ đổi ME/CE thành MC/ME mới đúng chứ nhỉ?)
Áp dụng định lý Talet trong 2 \(\Delta MBA\)và \(\Delta MDF\)ta có:
\(\frac{MB}{MD}=\frac{MA}{MF}\left(1\right)\)
Tương tự áp dụng Talet trong 2 tam giác MAC,MFE ta có:
\(\frac{MC}{ME}=\frac{MA}{MF}\left(2\right)\)
Từ (1) và (2) suy ra: (đpcm)
b) (A là trọng tâm của tam giác DEF)
Dễ dàng chứng minh: \(\frac{BC}{DE}=\frac{1}{3}\)(tự c/m)
tam giác ABC đồng dạng với tam giác FDE theo trường hợp g.g (tự c/m)
=> BC/DE=AB/DF=AC/EF=1/3
tam giác MBA đồng dạng với tam giác MDF theo trường hợp g.g (tự c/m)
=> MA/MF=AB/DF=1/3
=>3.AM=MF
=> (ĐPCM)