Giải hộ em đi ạ :333
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


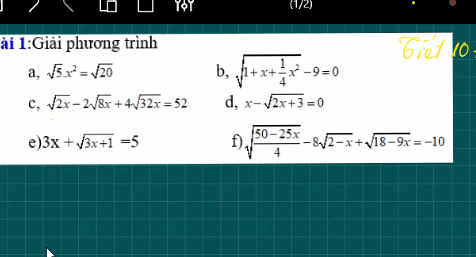
a) \(\Leftrightarrow x^2=\sqrt{4}\)
\(\Leftrightarrow x^2=2\Leftrightarrow x=\pm2\)
b) \(\Leftrightarrow\sqrt{\left(\dfrac{1}{2}x+1\right)^2}=9\)
\(\Leftrightarrow\left|\dfrac{1}{2}x+1\right|=9\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x+1=9\\\dfrac{1}{2}x+1=-9\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=-16\end{matrix}\right.\)
c) \(\Leftrightarrow\sqrt{2x}-4\sqrt{2x}+16\sqrt{2x}=52\left(đk:x\ge0\right)\)
\(\Leftrightarrow13\sqrt{2x}=52\Leftrightarrow\sqrt{2x}=4\Leftrightarrow2x=16\Leftrightarrow x=8\left(tm\right)\)
f: Ta có: \(\sqrt{\dfrac{50-25x}{4}}-8\sqrt{2-x}+\sqrt{18-9x}=-10\)
\(\Leftrightarrow\sqrt{2-x}\cdot\dfrac{5}{2}-8\sqrt{2-x}+3\sqrt{2-x}=-10\)
\(\Leftrightarrow\sqrt{2-x}=4\)
\(\Leftrightarrow2-x=16\)
hay x=-14


411 x 333...3 (có 70 chữ số 3) = 411 x 3 111...1 (có 70 chữ số 1)=1233 x 111....1(có 70 chữ số 1)

#\(N\)
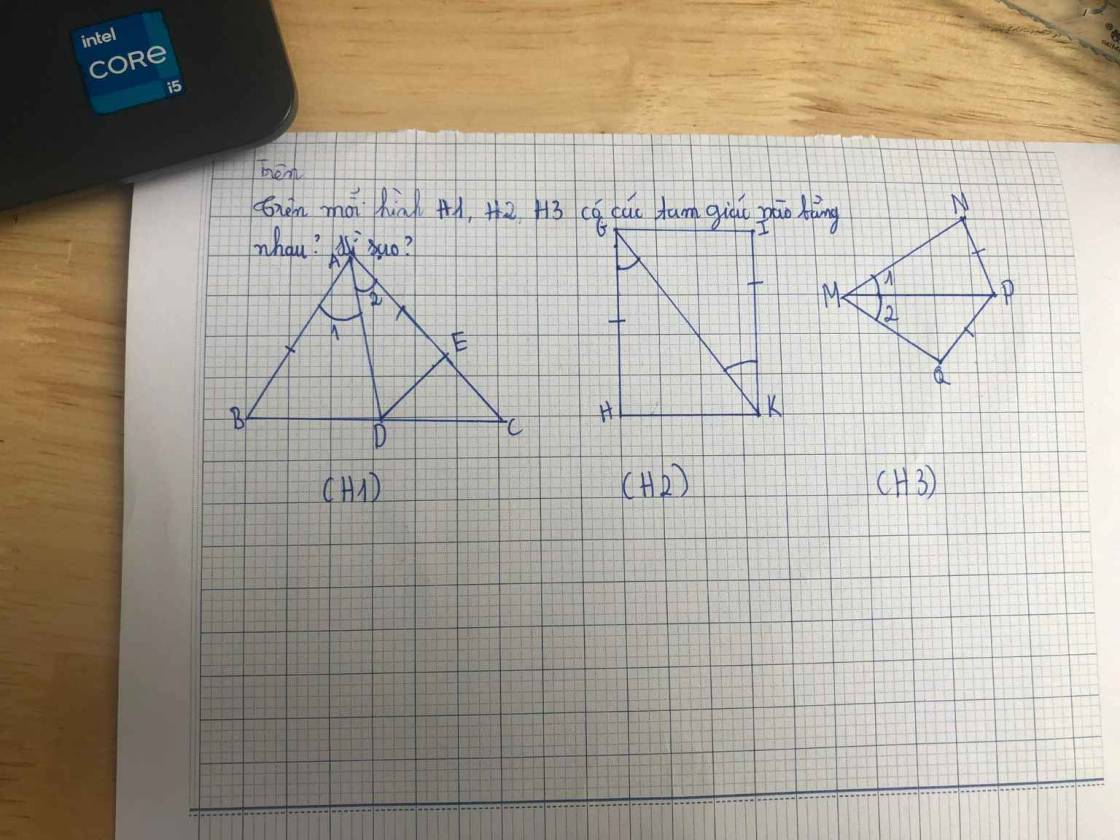
`H1,`
Xét Tam giác `ADB` và Tam giác `ADE`có:
`AB = AE`
\(\widehat{BAD}=\widehat{EAD}\)
`AD` chung
`=>` Tam giác `ADB = ` Tam giác `ADE (c-g-c)`
`H2,` Xét Tam giác `HGK` và Tam giác `IKG` có:
`HG = IK`
\(\widehat{HGK}=\widehat{IKG}\)
`GK` chung
`=>` Tam giác `HGK =` Tam giác `IKG (c-g-c)`
`H3,` Không có tam giác nào bằng nhau (vì 2 tam giác trên không có đủ yếu tố)
*ps: lần sau vẽ hình cân đối hơn cậu nha .-.

e) Ta có: \(\sqrt{9-4\sqrt{5}}+\dfrac{1}{\sqrt{5}-2}\)
\(=\sqrt{5}-2+\sqrt{5}+2\)
\(=2\sqrt{5}\)


chiếu:Mẹ em mới mua 1 cái chiếu rất đẹp.
Cái đèn nhà em chiếu rất sáng.
kho: Em rất thích ăn thịt kho tàu.
Nhà em mới xây thêm một cái nhà kho.

a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
Do đó: ΔABD=ΔACD
b: ΔABD=ΔACD
=>\(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
c: Ta có: \(\widehat{ADB}=90^0\)
=>AD\(\perp\)BC tại D
D là trung điểm của BC
=>\(DB=DC=\dfrac{BC}{2}=\dfrac{24}{2}=12\left(cm\right)\)
ΔADB vuông tại D
=>\(AD^2+DB^2=AB^2\)
=>\(AD^2=20^2-12^2=256\)
=>\(AD=\sqrt{256}=16\left(cm\right)\)
Xét ΔABC có
AD là đường trung tuyến
G là trọng tâm
Do đó: \(AG=\dfrac{2}{3}AD=\dfrac{2}{3}\cdot16=\dfrac{32}{3}\left(cm\right)\)



1A
\(a,\left(2x+3\right)^2=4x^2+12x+9\)
\(b,\left(6-3n\right)^2=36-36n+9n^2\)
\(c,\left(y-4\right)\left(y+4\right)=y^2-16\)
\(d,\left(\frac{a}{2}-4\right)^2=\frac{a^2}{4}-4a+16\)
1B
\(a,\left(x-\frac{3}{4}\right)^2=x^2-\frac{3}{2}x+\frac{9}{16}\)
\(b,\left(3t+1\right)^2=9t^2+6t+1\)
\(c,\left(3a+\frac{1}{3}\right)\left(\frac{1}{3}-3a\right)=\frac{1}{9}-9a^2\)
\(d,\left(a^2-2\right)^2=a^4-4a^2+4\)
2A
\(a,\left(\frac{a}{3}+4y\right)^2=\frac{a^2}{9}+\frac{8a}{3}y+16y^2\)
\(b,\left(\frac{1}{x}-\frac{3}{y}\right)^2=\frac{1}{x^2}-\frac{6}{xy}+\frac{9}{y^2}\)
\(c,\left(\frac{x}{2}-\frac{yz}{6}\right)\left(\frac{x}{2}+\frac{yz}{6}\right)=\frac{x^2}{4}-\frac{y^2x^2}{36}\)
\(d,\left(x^2+\frac{2}{5}y\right)\left(x^2-\frac{2}{5}y\right)=x^4-\frac{4}{25}y^2\)
2B
\(a,\left(y-2xy\right)^2=y^2-4xy^2+4x^2y^2\)
\(b,16\left(-\frac{1}{4}x+\frac{3}{5}y\right)^2=16\left(\frac{9}{25}y^2-\frac{3}{10}xy+\frac{1}{16}x^2\right)=\frac{144}{25}y^2-\frac{48}{10}xy+x^2\)
\(c,\left(-\frac{1}{3}ab^2+c^3\right)\left(-\frac{1}{3}ab^2-c^3\right)=\frac{1}{9}a^2b^4-c^6\)
\(d,\left(a+\frac{2}{3}\right)^2\left(a-\frac{2}{3}\right)^2=\left(a^2-\frac{4}{9}\right)^2=a^4-\frac{8}{9}a+\frac{16}{81}\)