cba+ab+cb=899
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC và ΔDEC có
CA=CD
\(\widehat{ACB}=\widehat{DCE}\)
CB=CE
Do đó:ΔACB=ΔDCE
b: Xét tứ giác ABDE có
C là trung điểm của AD
C là trung điểm của BE
Do đó: ABDE là hình bình hành
Suy ra: AB//DE
c: Xét ΔAMC và ΔDNC có
AM=DN
\(\widehat{MAC}=\widehat{NDC}\)
AC=DC
Do đó: ΔAMC=ΔDNC
d: Xét tứ giác AMDN có
AM//DN
AM=DN
Do đó: AMDN là hình bình hành
Suy ra: Hai đường chéo AD và MN cắt nhau tại trung điểm của mỗi đường
mà C là trung điểm của AD
nên C là trung điểm của MN
https://hoc24.vn/cau-hoi/1cho-tam-giac-abc-co-2-duong-trung-tuyen-bm-va-cn-cat-nhau-tai-g-chung-minh-bm-cn-dfrac32bc2cho-tam-giac-abc-d-la-trung-diem-ac-tren-bd-lay-e-sao-cho-be2ed-f-thuoc-tia-doi-cua-tia.5863553679489
trl câu này hộ mik với chiều nay cần dùng r![]()

a) Xét \(\Delta ABH\) và \(\Delta CBA\)có:
\(\widehat{AHB}=\widehat{CAB}=90^0\)
\(\widehat{ABC}\) CHUNG
Suy ra: \(\Delta ABH~\Delta CBA\)
\(\Rightarrow\)\(\frac{AB}{CB}=\frac{BH}{AB}\)
\(\Rightarrow\)\(AB^2=BH.CB\)
b) \(\Delta ABH~\Delta CBA\)
\(\Rightarrow\)\(\frac{AB}{BC}=\frac{HB}{AB}\)
\(\Rightarrow\)\(AB^2=BC.HB=12.4=48\)
\(\Rightarrow\)\(AB=\sqrt{48}=4\sqrt{3}\)
Áp dụng định lý Pytago vào tam giác vuông ABC ta có:
\(AC^2=BC^2-AB^2\)
\(\Leftrightarrow\)\(AC^2=12^2-\left(4\sqrt{3}\right)^2=96\)
\(\Leftrightarrow\)\(AC=\sqrt{96}=4\sqrt{6}\)

Ta có: \(\widehat {ACB} + \widehat {ACx} = {180^o}\, \Rightarrow \widehat {ACx} = 180 - \widehat {ACB}\)
\(\widehat {BAC} + \widehat {CBA} + \widehat {ACB} = {180^o} \Rightarrow \widehat {BAC} + \widehat {CBA} = {180^o} - \widehat {ACB}\)
Vậy \(\widehat {ACx} = \widehat {BAC} + \widehat {CBA}\)

Chọn D.
Phương pháp: Tính tích phân để suy ra a, b, c.
Cách giải: Ta có:
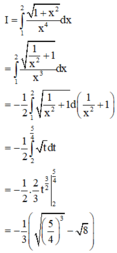
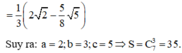
trả lời đi