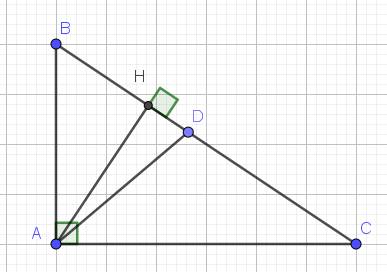
Cho tam giác ABC vuông tại A,AB=6cm AC=8cm, đường cao AH
a) Tính BC; AH
b) Qua H kẻ HE vuông góc với AB, HF vuông góc với AC. Tính EF
c) Gọi M,N lần lượt là trung điểm của HB, HC. Tứ giác MNFE là hình gì? Tính diện tích của tứ giác MNFE

a: BC=10cm
AH=4,8cm
b: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
Suy ra: AH=EF=4,8cm