\(1+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{50}}< 10\sqrt{2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NL
30 tháng 9 2018
Đặt B = \(1+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{50}}\)
= \(1+2\left(\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}+...+\dfrac{1}{2\sqrt{50}}\right)\)
Đặt \(A=\dfrac{1}{2\sqrt{2}}+\dfrac{1}{2\sqrt{3}}+...+\dfrac{1}{2\sqrt{50}}\)
Xét A < \(\dfrac{1}{\sqrt{1}+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+...+\dfrac{1}{\sqrt{49}+\sqrt{50}}\)
=> A < \(\dfrac{\sqrt{2}-\sqrt{1}}{1}+\dfrac{\sqrt{3}-\sqrt{2}}{1}+...+\dfrac{\sqrt{50}-\sqrt{40}}{1}\)
=> A < -1 + \(\sqrt{50}\)
=> 2A < -2 + \(10\sqrt{2}\)
=> 2A + 1 = B < -2 + \(10\sqrt{2}\) + 1
=> B < -1 + \(10\sqrt{2}\) < \(10\sqrt{2}\) (1)
Xét \(\dfrac{1}{\sqrt{n}}>2\left(\sqrt{n+1}-\sqrt{n}\right)\)
=> \(\dfrac{1}{\sqrt{1}}>2\left(\sqrt{2}-\sqrt{1}\right)\)
\(\dfrac{1}{\sqrt{2}}>2\left(\sqrt{3}-\sqrt{2}\right)\)
\(\dfrac{1}{\sqrt{3}}>2\left(\sqrt{4}-\sqrt{3}\right)\)
...
\(\dfrac{1}{\sqrt{50}}>2\left(\sqrt{51}-\sqrt{50}\right)\)
=> B > 2(\(\sqrt{51}-\sqrt{1}\))
=> B >-2 + \(10\sqrt{2}\) > \(5\sqrt{2}\)
5 tháng 10 2018
Cảm ơn bạn nha. Mà bạn bị nhầm 49 thành 40 ở dòng thứ 5 đó.
16 tháng 10 2021
a: Ta có: \(A=\sqrt{8}-2\sqrt{18}+3\sqrt{50}\)
\(=2\sqrt{2}-6\sqrt{2}+15\sqrt{2}\)
\(=11\sqrt{2}\)
b: Ta có: \(B=\sqrt{125}-10\sqrt{\dfrac{1}{20}}+\dfrac{5-\sqrt{5}}{\sqrt{5}}\)
\(=5\sqrt{5}-\sqrt{5}+\sqrt{5}-1\)
\(=5\sqrt{5}-1\)
5 tháng 10 2021
a: Ta có: \(\left(4\sqrt{2}-\dfrac{11}{2}\sqrt{8}-\dfrac{1}{3}\sqrt{288}+\sqrt{50}\right)\cdot\left(\dfrac{1}{2}\sqrt{2}\right)\)
\(=\dfrac{1}{2}\sqrt{2}\cdot\left(4\sqrt{2}-11\sqrt{2}-4\sqrt{2}+5\sqrt{2}\right)\)
\(=\dfrac{1}{2}\sqrt{2}\cdot6\sqrt{2}=3\)
H9
HT.Phong (9A5)
CTVHS
14 tháng 8 2023
\(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\dfrac{5-2\sqrt{5}}{2\sqrt{5}-4}\)
\(=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{5}\left(\sqrt{5}-2\right)}{2\left(\sqrt{5}-2\right)}\)
\(=\sqrt{5}+\dfrac{\sqrt{5}}{2}\)
\(=\dfrac{2\sqrt{5}}{2}+\dfrac{\sqrt{5}}{2}\)
\(=\dfrac{3\sqrt{5}}{2}\)
H9
HT.Phong (9A5)
CTVHS
14 tháng 8 2023
\(\left(\sqrt{3}+1\right)\cdot\dfrac{\sqrt{3}-3}{2\sqrt{3}}\)
\(=\left(\sqrt{3}+1\right)\cdot\dfrac{\sqrt{3}\left(1-\sqrt{3}\right)}{2\sqrt{3}}\)
\(=\left(\sqrt{3}+1\right)\cdot\dfrac{1-\sqrt{3}}{2}\)
\(=\dfrac{\left(1+\sqrt{3}\right)\left(1-\sqrt{3}\right)}{2}\)
\(=\dfrac{1-3}{2}\)
\(=-1\)
29 tháng 8 2021
Ta có: \(\left(\dfrac{1}{2}\sqrt{\dfrac{1}{2}}-\dfrac{3}{2}\cdot\sqrt{4.5}+\dfrac{2}{5}\sqrt{50}\right):\dfrac{4}{15}\sqrt{\dfrac{1}{8}}\)
\(=\left(\dfrac{1}{4}\sqrt{2}-\dfrac{9}{4}\sqrt{2}+2\sqrt{2}\right):\dfrac{\sqrt{2}}{15}\)
\(=0\)
22 tháng 9 2021
\(6\sqrt{\dfrac{1}{2}}+\dfrac{2}{\sqrt{2}}-\sqrt{50}=3\sqrt{2}+\sqrt{2}-5\sqrt{2}=-\sqrt{2}\\ \dfrac{2+\sqrt{3}}{2-\sqrt{3}}-\dfrac{2-\sqrt{3}}{2+\sqrt{3}}=\dfrac{\left(2+\sqrt{3}\right)^2-\left(2-\sqrt{3}\right)^2}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}\\ =\dfrac{7+4\sqrt{3}-\left(7-4\sqrt{3}\right)}{\left(2-\sqrt{3}\right)\left(2+\sqrt{3}\right)}=\dfrac{8\sqrt{3}}{1}=8\sqrt{3}\)
29 tháng 6 2021
`c)1/(2sqrt2)-3/2sqrt{4,5}+2/5sqrt{50}`
`=1/(2sqrt2)-3/2sqrt{9/2}+2/5sqrt{25.2}`
`=1/(2sqrt2)-9/(2sqrt2)+2sqrt2`
`=2sqrt2-8/(2sqrt2)`
`=2sqrt2-sqrt2=sqrt2`
`d)4/(3+sqrt5)-8/(1+sqrt5)+15/sqrt5`
`=(4(3-sqrt5))/(9-5)-(8(sqrt5-1))/(5-1)+3sqrt5`
`=3-sqrt5-2(sqrt5-1)+3sqrt5`
`=3+3sqrt5-3sqrt5+2=5`
11 tháng 4 2023
1: ĐKXĐ: x>1/2
=>\(\dfrac{x}{\sqrt{2x-1}}+\dfrac{x}{\sqrt[4]{4x-3}}=2\)
x^2-2x+1>=0
=>x^2>=2x-1
=>\(\dfrac{x}{\sqrt{2x-1}}>=1\)
Dấu = xảy ra khi x=1
(x^2-2x+1)(x^2+2x+3)>=0
=>x^4-4x+3>=0
=>x^4>=4x-3
=>\(\dfrac{x}{\sqrt[4]{4x-3}}>=1\)
=>VT>=2
Dấu = xảy ra khi x=1
2: 4x-1=x+x+2x-1
5x-2=x+2x-1+2x-1
\(\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}\right)\left(\sqrt{x}+\sqrt{x}+\sqrt{2x-1}\right)>=9\)
=>\(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}>=\dfrac{9}{\sqrt{x}+\sqrt{x}+\sqrt{2x-1}}\)
\(\left(\sqrt{x}+\sqrt{x}+\sqrt{2x-1}\right)^2< =3\left(4x-1\right)\)
=>\(\sqrt{x}+\sqrt{x}+\sqrt{2x-1}< =\sqrt{3\left(4x-1\right)}\)
=>\(\dfrac{2}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}>=\dfrac{3\sqrt{3}}{\sqrt{4x-1}}\)
Tương tự, ta cũng có: \(\dfrac{1}{\sqrt{x}}+\dfrac{2}{\sqrt{2x-1}}>=\dfrac{3\sqrt{3}}{\sqrt{5x-2}}\)
=>\(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{2x-1}}>=\sqrt{3}\left(\dfrac{1}{\sqrt{4x-1}}+\dfrac{1}{\sqrt{5x-2}}\right)\)
Dấu = xảy ra khi x=1
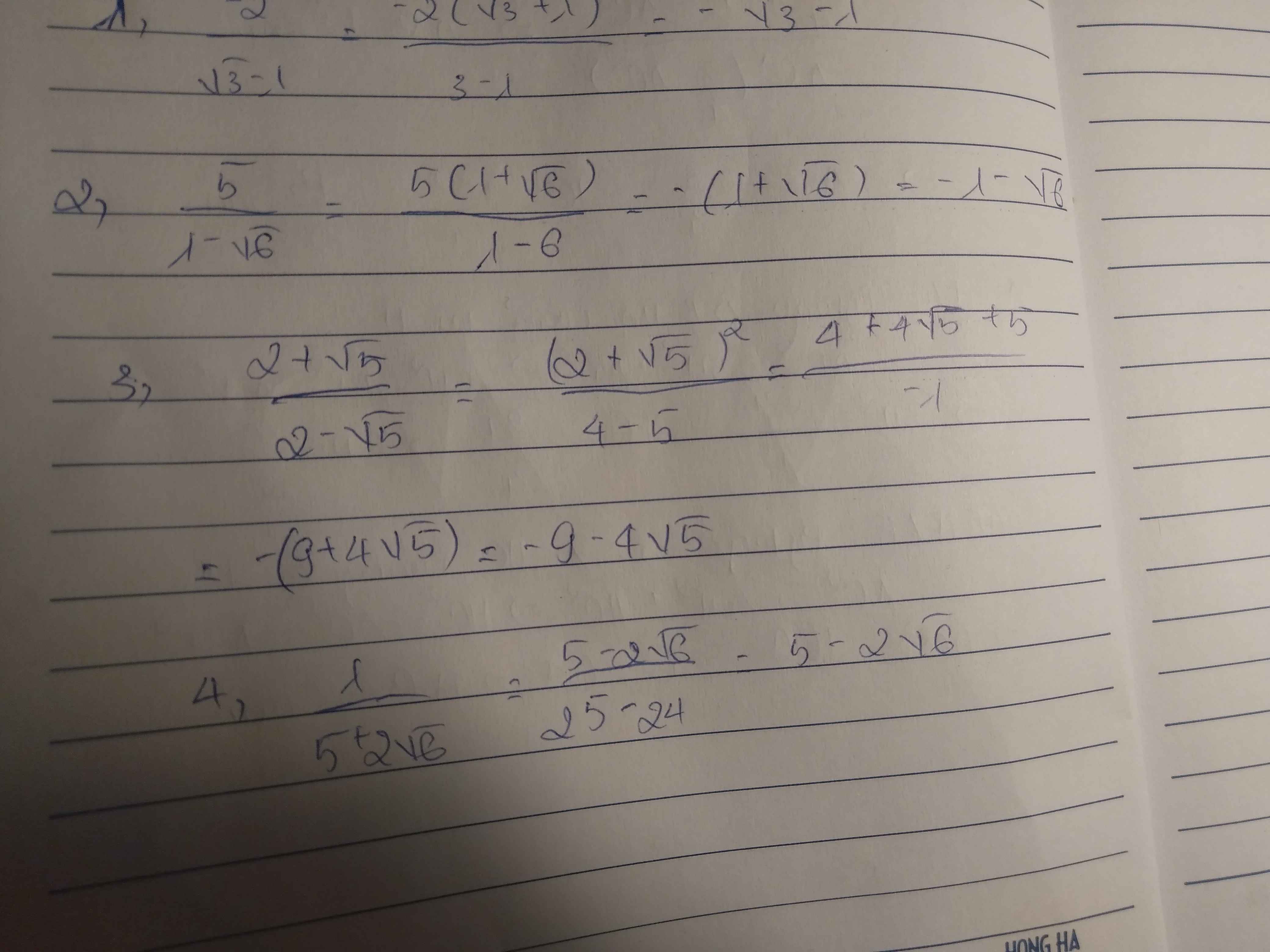
Vời mọi k > 0 , ta có:
\(\dfrac{1}{\sqrt{k}}=\dfrac{2}{\sqrt{k}+\sqrt{k}}< \dfrac{2}{\sqrt{k}+\sqrt{k-1}}=2\left(\sqrt{k}-\sqrt{k-1}\right)\)
\(A=\dfrac{1}{\sqrt{1}}+\dfrac{1}{\sqrt{2}}+\dfrac{1}{\sqrt{3}}+...+\dfrac{1}{\sqrt{50}}\)
\(\Rightarrow A< 2\left[\left(\sqrt{50}-\sqrt{49}\right)+...+\left(\sqrt{2}-\sqrt{1}\right)+\left(\sqrt{1}-0\right)\right]\)
\(\Rightarrow A< 2\left(\sqrt{50}-0\right)=2\sqrt{50}=10\sqrt{2}\)(đpcm)
cú đêm :))