Cho hình thoi ABCD có A = 60 độ . kẻ 2 đường cao BE va BF. Tam giác BEF là tam giác gì
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






Bài làm
A B C D E F 60 o
Xét tam giác AEB và tam giác DFB có:
\(\widehat{BEA}=\widehat{BFD}=90^0\)
Cạnh huyền AB = BD ( Do ABCD là hình thoi nên AB = AC = CD = BD )
Góc nhọn: \(\widehat{A}=\widehat{D}\)( hai góc đối của hình thoi )
=> Tam giác AEB = tam giác DFB ( cạnh huyền - góc nhọn )
=> BE = BF ( hai cạnh tương ứng )
=> Tam giác BEF cân tại B.
Xét tam giác ABE vuông tại E có:
\(\widehat{A}+\widehat{ABE}=90^0\)( hai góc phụ nhau )
hay \(60^0+\widehat{ABE}=90^0\)
=> \(\widehat{ABE}=90^0-60^0=30^0\)
Mà \(\widehat{ABE}=\widehat{DBF}=30^0\)( Vì tam giác AEB = tam giác DFB )
Ta có: \(\widehat{ABD}+\widehat{BDC}=180^0\)( Do BA // DC và hai góc này là hai góc trong cùng phía bù nhau )
=> \(\widehat{ABE}+\widehat{EBF}+\widehat{FBD}+\widehat{BDC}=180^0\)
hay \(30^0+\widehat{EBF}+30^0+60^0=180^0\)
=> \(\widehat{EBF}=180^0-60^0-30^0-30^0\)
=> \(\widehat{EBF}=60^0\)
Mà tam giác EBF cân tại B ( chứng minh trên )
=> Tam giác EBF là tam giác đều.


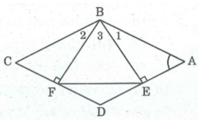
Xét hai tam giác vuông BEA và BFC, ta có:
∠ (BEA) = ∠ (BFC) = 90 0
∠ A = ∠ C (tính chất hình thoi)
BA = BC (gt)
Suy ra: ∆ BEA = ∆ BFC (cạnh huyền, góc nhọn)
Do đó, ta có:
* BE = BF ⇒ ΔBEF cân tại B
* ∠ B 1 = ∠ B 2
Trong tam giác vuông BEA, ta có:
∠ A + ∠ B1= 90 0 ⇒ ∠ B1= 90 0 – ∠ A = 90 0 - 60 0 = 30 0
⇒ ∠ B 2 = ∠ B 1 = 30 0
∠ A + ∠ (ABC) = 180 0 (hai góc trong cùng phía bù nhau)
⇒ ∠ (ABC) = 180 0 – ∠ A = 180 0 - 60 0 = 120 0
⇒ ∠ (ABC) = ∠ B 1 + ∠ B 2 + ∠ B 3
⇒ ∠ B 3 = ∠ (ABC) – ( ∠ B 1 + ∠ B 2 ) = 120 0 - 30 0 + 30 0 = 60 0
Tam giác BEF cân tại B có ∠ (EBF) = 60 0 nên ∆ BEF đều.
