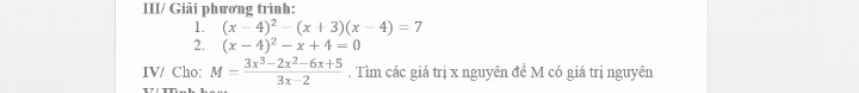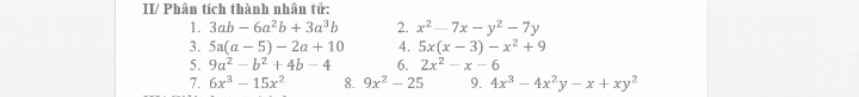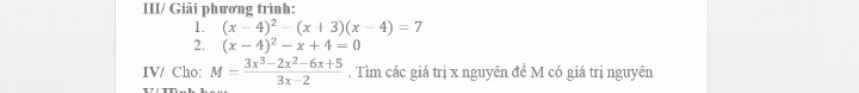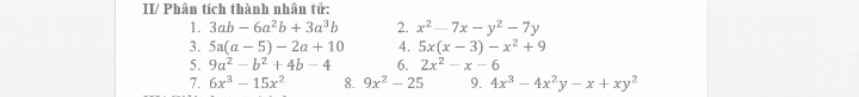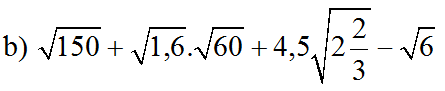Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





\(1,\Leftrightarrow x^2-8x+16-x^2+x+12=7\\ \Leftrightarrow-7x=-21\\ \Leftrightarrow x=3\\ 2,\Leftrightarrow\left(x-4\right)^2-\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(x-5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)

\(1,=3ab\left(1-2a+b\right)\\ 2,=\left(x-y\right)\left(x+y\right)-7\left(x+y\right)=\left(x+y\right)\left(x-y-7\right)\\ 3,=\left(a-5\right)\left(5a-2\right)\\ 4,=5x\left(x-3\right)-\left(x-3\right)\left(x+3\right)=\left(x-3\right)\left(4x-3\right)\\ 5,=9a^2-\left(b-2\right)^2=\left(3a-b+2\right)\left(3a+b-2\right)\\ 6,=2x^2-4x+3x-6=\left(x-2\right)\left(2x+3\right)\\ 7,=3x^2\left(2x-5\right)\\ 8,=\left(3x-5\right)\left(3x+5\right)\\ 9,=4x^2\left(x-y\right)-x\left(x-y\right)=x\left(4x-1\right)\left(x-y\right)\)




b) Ta có: \(\sqrt{150}-\sqrt{1.6}\cdot\sqrt{60}+4.5\cdot\sqrt{2\dfrac{2}{3}}-\sqrt{6}\)
\(=5\sqrt{6}-4\sqrt{6}-\sqrt{6}+\dfrac{9}{2}\cdot\sqrt{\dfrac{8}{3}}\)
\(=\dfrac{9}{2}\cdot\dfrac{2\sqrt{2}}{\sqrt{3}}\)
\(=3\sqrt{6}\)
\(\sqrt{150}+\sqrt{1,6}.\sqrt{60}+4.5\sqrt{2\dfrac{2}{3}}-\sqrt{6}\\ =5\sqrt{6}+4\sqrt{6}+3\sqrt{6}-\sqrt{6}\\ =11\sqrt{6}\)

\(a,\Leftrightarrow2x\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
\(b,\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}3+x>0\\2x-5>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+3< 0\\2x-5< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{5}{2}\\x< -3\end{matrix}\right.\)
\(c,\Leftrightarrow x\left(x+3\right)< 0\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x< 0\\x+3>0\end{matrix}\right.\\\left\{{}\begin{matrix}x>0\\x+3< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow-3< x< 0\)
\(d,\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3>0\\x+5>0\end{matrix}\right.\\\left\{{}\begin{matrix}x+3< 0\\x+5< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x>-3\\x< -5\end{matrix}\right.\)
\(e,\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}3-2x\ge0\\x-1>0\end{matrix}\right.\\\left\{{}\begin{matrix}3-2x\le0\\x-1< 0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\le\dfrac{3}{2}\\x>1\end{matrix}\right.\\\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x< 1\end{matrix}\right.\end{matrix}\right.\Leftrightarrow1< x\le\dfrac{3}{2}\)