Tìm nghiệm nguyên của phương trình:
x4 - 2y4 - x2y2 - 4x2 - 7y2 - 5 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 11 2018
Đáp án A
Bất phương trình ⇔ x 4 − 4 x 2 + 4 ≤ x 2 − 2 2 ≤ m + 3
Để bất phương trình có nghiệm thực thì m + 3 ≥ min x 2 − 2 2 = 0 ⇔ m ≥ − 3
BN
0
CM
4 tháng 9 2018
Đáp án C.
Xét hàm số x 4 - 4 x 2 + 5 ⇒ y ' = 0
⇔ 4 x 3 - 8 x = 0 ⇔ x = 0 x = ± 2
Bảng biến thiên:
⇒ Đồ thị hàm số y = x 4 - 4 x 2 - 5 ( C )
Từ (C) giữ phần đồ thị phía trên, bỏ phía dưới sau khi lấy đối xứng qua Ox
⇒ Đồ thị hàm số y = x 4 - 4 x 2 - 5 (hình vẽ)
⇒ Phương trình y = x 4 - 4 x 2 - 5 = m có 6 nghiệm ⇔ 5 < m < 9 ⇒ a + b = 14 .
CM
30 tháng 11 2017
Chọn đáp án B
Ta có
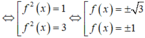
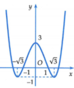
Quan sát đồ thị của hàm số y = f(x) ta thấy:
Phương trình f x = - 3 không có nghiệm; phương trình f x = - 1 có 2 nghiệm;
phương trình f x = 1 có 4 nghiệm; phương trình f x = 3 có 4 nghiệm.
Vậy phương trình x 4 - 4 x 2 + 3 2 - 4 x 4 - 4 x 2 + 3 2 + 3 = 0 có 10 nghiệm.
Biến đổi đưa được pt về dạng: (x2 – 2y2 – 5)(x2 + y2 +1) = 0
\(\Leftrightarrow\)x2 – 2y – 5 = 0
\(\Leftrightarrow\)x2 = 2y2 + 5
\(\Leftrightarrow\)x lẻ
Đặt x = 2k + 1 ; ( k \(\in Z\))
\(\Leftrightarrow\)4k2 + 4k +1 = 2y2 + 5
\(\Leftrightarrow\)2y2 = 4k2 + 4k – 4
\(\Leftrightarrow\)y2 = 2(k2 + k – 1)
\(\Leftrightarrow\)y chẵn
Đặt y = 2n; (n \(\in Z\))
\(\Leftrightarrow\)4n2 = 2(k2 + k – 1)
\(\Leftrightarrow\)2n2 + 1 = k(k + 1) (*)
- Nhìn vào (*) ta có nhận xét:
+Vế trái nhận giá trị lẻ, vế phải nhận giá trị chẵn (Vì k và k + 1 là hai số nguyên liên tiếp)
\(\Leftrightarrow\)(*) vô nghiệm
\(\Leftrightarrow\)pt đã cho vô nghiệm