AB=15,AH=12 tinhs AC,BC,BH,HC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 9 2021
Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{4}\)
\(\Leftrightarrow HB=\dfrac{9}{16}HC\)
Ta có: HB+HC=BC
\(\Leftrightarrow HC\cdot\dfrac{25}{16}=15\)
\(\Leftrightarrow HC=9.6\left(cm\right)\)
hay HB=5,4(cm)
ND
1
13 tháng 3 2017
TA CÓ TAM GIÁC ABH VUÔNG TẠI H ;A/D ĐỊNH LÝ PYTAGO TA CÓ
\(AB^2=AH^2+BH^2=>BH^2=AB^2-AH^2\)
=>\(BH^2=15^2-12^2=>BH^2=81=>BH=9'\left(cm\right)\)
=>\(BC=9+16=25\left(cm\right)\)
ta có \(\Delta AHC\) VUÔNG TẠI H A/D ĐỊNHLÝ PYTAGO TA CÓ
\(AC^2=AH^2+HC^2=>AC^2=12^2+16^2\)
=>\(AC^2=400=>AC=20\left(cm\right)\)
24 tháng 5 2023
a: CH=16^2/25=10,24cm
BC=25+10,24=35,24cm
AB=căn 16^2+25^2=căn 881(cm)
b: AH=căn 12^2-6^2=6căn 3cm
CH=AH^2/HB=108/6=18cm
BC=6+18=24cm
c: BC=căn 5^2+25^2=5 căn 26cm
BH=5^2/5căn 26=5/căn 26(cm)
CH=5căn 26-5/căn 26=24,51(cm)
d: AB=căn 16^2-14^2=2căn15(cm)
e: AB=căn 2*8=4cm
AC=căn 6*8=4căn 3(cm)
11 tháng 7 2021
f) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB\cdot HC=12^2=144\)(1)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên BH+CH=25
hay BH=25-CH(2)
Thay (2) vào (1), ta được:
\(HC\left(25-HC\right)=144\)
\(\Leftrightarrow HC^2-25HC+144=0\)
\(\Leftrightarrow\left[{}\begin{matrix}HC=16\\HC=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}HB=9\\HB=16\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AB\in\left\{15;20\right\}\\AC\in\left\{20;15\right\}\end{matrix}\right.\)
LP
4
10 tháng 7 2021
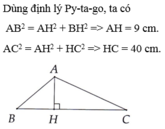
Áp dụng định lý Pi-ta-go vào tam giác vuông ABH vuông tại H ta có:
AB2= BH2 + AH2
<=> 152= 122+ AH2
<=> AH2= 152- 122= 225- 144= 81
<=> AH= 9 (cm)
Tương tự ta có : Áp dụng định lý Pi-ta-go vào tam giác vuông ACH vuông tại H .
AC2= AH2+ HC2
<=> 412= 92+ HC2
<=> HC2= 412- 92= 1681- 81= 1600
<=>HC= 40 (cm)
25 tháng 2 2020
Xét △AHB vuông tại H có:
\(AB^2=AH^2+HB^2\) (định lí Pytago)
\(\Rightarrow15^2=AH^2+12^2\\ \Rightarrow AH^2=225-144=81\\ \Rightarrow AH=9\left(cm\right)\)
Xét △AHC vuông tại H có:
\(AC^2=AH^2+HC^2\) (định lí Pytago)
\(\Rightarrow41^2=9^2+HC^2\\ \Rightarrow HC^2=1681-81=1600\\ \Rightarrow HC=40\left(cm\right)\)
TG
25 tháng 2 2020
ΔABH vuông tại H. Áp dụng định lý Pitago ta có:
\(AB^2=BH^2+AH^2\)
\(\Rightarrow AH^2=AB^2-BH^2=15^2-12^2=225-144=81=9^2\)
=> AH = 9
ΔACH vuông tại H. Áp dụng định lý Pitago ta có:
\(AC^2=AH^2-HC^2\)
=> \(HC^2=AC^2-AH^2=41^2-9^2=1681-81=1600\)
=> HC = \(\sqrt{1600}=40\)
Vậy: HC = 40
H9
HT.Phong (9A5)
CTVHS
5 tháng 8 2023
Áp dụng hệ thức đường cao và hình chiếu ta có:
\(AH^2=BH\cdot HC\)
\(\Rightarrow AH^2=BH\cdot\left(BC-BH\right)\)
\(\Rightarrow12^2=BH\cdot\left(25-BH\right)\)
\(\Rightarrow144=25\cdot BH-BH^2\)
\(\Rightarrow BH^2-25\cdot BH+144=0\)
\(\Rightarrow\left(BH-9\right)\left(BH-16\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}BH=9\left(cm\right)\\BH=16\left(cm\right)\end{matrix}\right.\)
(1) Với: BH=9(cm)
\(\Rightarrow HC=BC-HB=25-9=16\left(cm\right)\)
Áp dụng hệ thức cạnh góc vuông và hình chiếu ta có:
\(AB^2=BH\cdot BC\Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{9\cdot25}=15\left(cm\right)\)
\(AC^2=HC\cdot BC\Rightarrow AC=\sqrt{HC\cdot BC}=\sqrt{16\cdot25}=20\left(cm\right)\)
(2) Với BC=16(cm)
\(\Rightarrow HC=BC-BH=25-16=9\left(cm\right)\)
Áp dụng hệ thức cạnh góc vuông và hình chiếu ta có:
\(AB^2=BH\cdot BC\Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{16\cdot25}=20\left(cm\right)\)
\(AC^2=HC\cdot BC\Rightarrow AB=\sqrt{HC\cdot BC}=\sqrt{9\cdot25}=15\left(cm\right)\)
Đề thiếu. Bạn coi lại đề.
Ta có: AB2=AH2+BH2⇔ BH2=AB2-AH2=152-122 = 81
⇔ BH = 9 cm
Ta có:\(AB^2=BH.BC\Leftrightarrow BC=\dfrac{AB^2}{BH}=\dfrac{15^2}{9}=25\left(cm\right)\)
Ta có: BC=BH+HC ⇔ HC=BC-BH=25-9=16 cm
Ta có: BC2=AB2+AC2⇔ AC2=BC2-AB2=252-152=400
⇔ AC = 20 cm