tìm tham số m để bất phương trình mx2 -mx -5 <0 có tập nghiệm là R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 3 2022
Để bất phương trình có tập nghiệm là R thì \(\left(m-2\right)^2-4\left(m+1\right)< 0\)
\(\Rightarrow m^2-4m+4-4m-4< 0\)
=>m(m-8)<0
=>0<m<8
HN
16 tháng 3 2022
Để bất phương trình đã cho có tập nghiệm là R thì
\(\left\{{}\begin{matrix}a>0\\\Delta\le0\end{matrix}\right.\) (với a là hệ số của x2 và bằng 1, thỏa)
\(\Rightarrow\) (m-2)2-4.(m+1)\(\le\)0 \(\Leftrightarrow\) m2-8m\(\le\)0 \(\Leftrightarrow\) 0\(\le\)m\(\le\)8.
CM
9 tháng 9 2017
Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.
Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi
∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4
Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4
Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.
Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.
Đáp án cần chọn là: A
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 2 2021
1.
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=\left(m+1\right)^2-4m\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-3m^2+7m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow m< \dfrac{7-\sqrt{61}}{6}\)
2.
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\3m^2+13m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4\le m\le-\dfrac{1}{3}\end{matrix}\right.\)
Không tồn tại m thỏa mãn
CM
6 tháng 11 2019
Bất phương trình x2-3x+2 ≤ 0 ⇔ 1 ≤ x ≤ 2
Bất phương trình mx2+(m+1) x+m+1 ≥ 0
Xét hàm số f ( x ) = - x - 2 x 2 + x + 1 , 1 ≤ x ≤ 2
Có f ' ( x ) = x 2 + 4 x + 1 ( x 2 + x + 1 ) 2 > 0 ∀ x ∈ 1 ; 2
Yêu cầu bài toán ⇔ m ≥ m a x [ 1 ; 2 ] f ( x ) ⇔ m ≥ - 4 7
Chọn C.
CM
5 tháng 10 2017
Giải bất phương trình x2- 3x+ 2≤ 0 ta được 1≤x≤2.
Bất phương trình mx2+ (m+ 1) x+ m+1≥0
⇔ m ( x 2 + x + 1 ) ≥ - x - 2 ⇔ m ≥ - x - 2 x 2 + x + 1
Xét hàm số f ( x ) = - x - 2 x 2 + x + 1 với 1≤ x≤ 2
Có đạo hàm f ' ( x ) = x 2 + 4 x + 1 ( x 2 + x + 1 ) 2 > 0 , ∀ x ∈ 1 ; 2
Yêu cầu bài toán ⇔ m ≥ m a x [ 1 ; 2 ] f ( x ) ⇔ m ≥ - 4 7
Chọn C.
QP
1
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 2 2021
\(\Leftrightarrow\dfrac{mx^2-5x+m-4}{mx^2-4x+m-3}>0\)
BPT đã cho có tập nghiệm là R khi và chỉ khi:
\(\left\{{}\begin{matrix}\Delta_1=25-4m\left(m-4\right)< 0\\\Delta'_2=4-m\left(m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-4m^2+16m+25< 0\\-m^2+3m+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< \dfrac{4-\sqrt{41}}{2}\\m>\dfrac{4+\sqrt{41}}{2}\end{matrix}\right.\)
CM
2 tháng 12 2019
Bất phương trình ( m 2 - m ) x < m vô nghiệm khi và chỉ khi m 2 - m = 0 m ≤ 0 ⇔ [ m = 0 m = 1 ⇔ m = 0 m ≤ 0
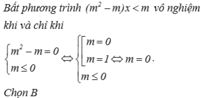
ta có phương trình \(mx^2-mx-5< 0\) có tập nghiệm là \(R\) khi \(\left\{{}\begin{matrix}a< 0\\\Delta< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\left(-m\right)^2-4m\left(-5\right)< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\m^2+20m< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-20< m< 0\end{matrix}\right.\) \(\Leftrightarrow-20< m< 0\)
vậy \(-20< m< 0\) thì bất phương trình \(mx^2-mx-5< 0\) có tập nghiệm là \(R\)