Rút gọn biểu thức : \(\sqrt{4+\sqrt{8}}\times\sqrt{2+\sqrt{2}}\times\sqrt{2\times\sqrt{2}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 7 2017
được bạn ạ mình nhờ thầy giải ra mà bạn tính máy tính mới ko ra thôi
26 tháng 10 2020
a) \(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{12}-\sqrt{\left(-3\right)^2}\)
\(=\left|\sqrt{3}-2\right|+\sqrt{2^2\cdot3}-\sqrt{3^2}\)
\(=2-\sqrt{3}+2\sqrt{3}-3\)
\(=\sqrt{3}-1\)
b) \(\left(\sqrt{8}-3\sqrt{6}+\sqrt{2}\right)\cdot\sqrt{2}+\sqrt{108}\)
\(=\sqrt{16}-3\sqrt{12}+\sqrt{4}+\sqrt{6^2\cdot3}\)
\(=4-3\sqrt{2^2\cdot3}+2+6\sqrt{3}\)
\(=6-3\cdot2\sqrt{3}+6\sqrt{3}\)
\(=6-6\sqrt{3}+6\sqrt{3}=6\)
NN
26 tháng 10 2020
a) \(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{12}-\sqrt{\left(-3\right)^2}\)
\(=\left|\sqrt{3}-2\right|+\sqrt{3.4}-\sqrt{3^2}=2-\sqrt{3}+\sqrt{4}.\sqrt{3}-3\)
\(=2-\sqrt{3}+2\sqrt{3}-3=\sqrt{3}-1\)
b) \(\left(\sqrt{8}-3\sqrt{6}+\sqrt{2}\right).\sqrt{2}+\sqrt{108}\)
\(=\sqrt{8}.\sqrt{2}-3\sqrt{6}.\sqrt{2}+\sqrt{2}.\sqrt{2}+\sqrt{108}\)
\(=\sqrt{8.2}-3\sqrt{6.2}+2+\sqrt{36.3}\)
\(=\sqrt{16}-3\sqrt{12}+2+\sqrt{36}.\sqrt{3}\)
\(=\sqrt{4^2}-3\sqrt{4.3}+2+6\sqrt{3}\)
\(=4-3\sqrt{4}.\sqrt{3}+2+6\sqrt{3}\)
\(=4-6\sqrt{3}+2+6\sqrt{3}=6\)
16 tháng 7 2021
ĐKXĐ : \(0\le x\le1\)
\(A=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}\right)^2.\dfrac{x^2-1}{2}-\sqrt{1-x^2}\)
\(=\left(\dfrac{2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)^2.\dfrac{\left(x-1\right)\left(x+1\right)}{2}-\sqrt{\left(1-x\right)\left(1+x\right)}\)
\(=\dfrac{4x}{\left(x-1\right)^2}.\dfrac{\left(x-1\right)\left(x+1\right)}{2}-\sqrt{\left(1-x\right)\left(1+x\right)}\)
\(=\dfrac{2x}{x-1}-\sqrt{1-x}.\sqrt{1+x}\)
\(=\dfrac{2x-\sqrt{1-x^2}.\left(x-1\right)}{x-1}\)
21 tháng 8 2017
Bài 1 :
a) \(\sqrt{4\left(a-3\right)^2}+2\sqrt{\left(a^2+4a+4\right)}\)
= \(2\left|a-3\right|+2\left|a+2\right|\)
\(=2.\left(-a+3\right)+2\left(-a-2\right)\)
b) có sai đề ko ?
c) \(4x-\sqrt{8}+\dfrac{\sqrt{x^3+2x^2}}{\sqrt{x+2}}=4x-\sqrt{8}+\sqrt{\dfrac{x^2\left(x+2\right)}{x+2}}=4x-2\sqrt{4}+x=3x-2\sqrt{4}\)
22 tháng 10 2023
giải phương trình
a)\(\sqrt{x^8}=256\) b)\(\sqrt{x^2-2x+1}=x-1\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 11 2019
\(A=\sqrt{6+2\sqrt{6-2\sqrt{\left(\sqrt{3}+1\right)^2}}}\)
\(=\sqrt{6+2\sqrt{6-2\left(\sqrt{3}+1\right)}}\)
\(=\sqrt{6+2\sqrt{4-2\sqrt{3}}}\)
\(=\sqrt{6+2\sqrt{\left(\sqrt{3}-1\right)^2}}\)
\(=\sqrt{6+2\left(\sqrt{3}-1\right)}\)
\(=\sqrt{4+2\sqrt{3}}\)
\(=\sqrt{\left(\sqrt{3}+1\right)^2}=\sqrt{3}+1\)
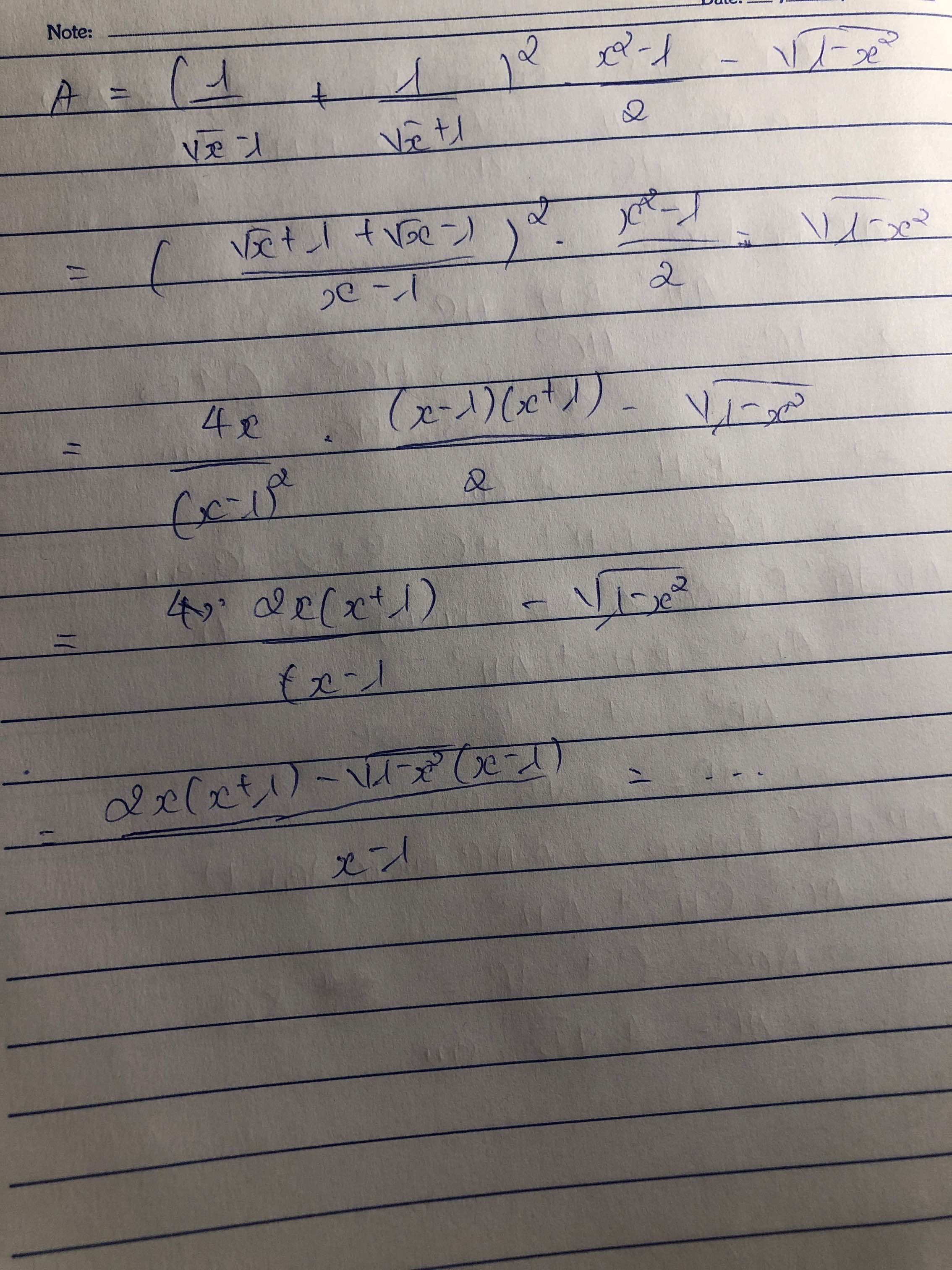
Sửa đề: \(\sqrt{4+\sqrt{8}}\cdot\sqrt{2+\sqrt{2}}\cdot\sqrt{2-\sqrt{2}}\)
\(=\sqrt{4+2\sqrt{2}}\cdot\sqrt{4-2}\)
\(=\sqrt{8+4\sqrt{2}}\)