Cho \(\Delta ABC\) cân tại A, \(\widehat{BAC}=20^o\). Trên nửa mặt phẳng bờ AC không chứa B vẽ Ax, Cy sao cho \(\widehat{CAx}=20^o,\widehat{ACy}=130^o.\) D là giao điểm của Ax, Cy. Trên nửa mặt phẳng bờ BD không chứa A, vẽ \(\Delta BDK\) cân tại B, \(\widehat{BDK}=50^o\). Chứng minh rằng A; B; K thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

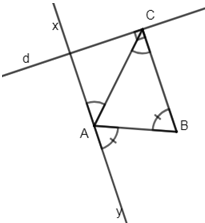
a) Ta có: mà hai góc đó là hai góc so le trong nên
suy ra (1)
mà hai góc đó là hai góc so le trong nên suy ra (2)
Từ (1) và (2) suy ra Ax và Ay cùng // BC.
Lại có tia Ax thuộc mặt phẳng bờ AB có chứa điểm C, tia Ay thuộc mặt phẳng
bờ AB không chứa điểm C
Ax và Ay là hai tia đối nhau.
b) Vì Ax và Ay là hai tia đối nhau (cmt) mà và
nên suy ra
Mà nên suy ra

a) Gọi I là trung điểm của AB,
K là trung điểm của AC.
Ta có:
\(IA=IE=MK=\frac{1}{2}AB\)
\(KF=KA=IM=\frac{1}{2}AC\)
TA CÓ TAM GIÁC IAE VÀ AKF LẦN LƯỢT CÂN TẠI I VÀ K
\(\Rightarrow\widehat{EIB}=2\widehat{xAB}=42^o;\widehat{CKF}=2\widehat{CAY}=42^o\)
\(\Rightarrow\widehat{EIB}=\widehat{CKF}\)
MI//AC
=> BIM=BAC ( đồng vị) (1)
M//AB
=> MKC=BAC (đồng vị)(2)
từ (1) và (2)
\(\Rightarrow\widehat{BIM}=\widehat{MKC}\)
TỪ ĐÂY TA CÓ THỂ DỄ DÀNG CÓ EIM=MKF
=> \(\Delta EIM\)= \(\Delta MKF\)
=> ME = MF
=> TAM GIÁC MEF cân tại M

Trên tia AM lấy điểm A’ sao cho AM = MA’
Dễ chứng minh được ∆AMC = ∆A’MB ( g.c.g)
A’B = AC ( = AE) và góc MAC = góc MA’B
AC // A’B => góc BAC + góc ABA’ = 180 0 (cặp góc trong cùng phía)
Mà góc DAE + góc BAC = 180 0 => góc DAE = góc ABA’
Xét ∆DAE và ∆ABA’ có : AE = A’B , AD = AB (gt)
góc DAE = góc ABA’ ∆DAE = ∆ABA’(c.g.c)
góc ADE = góc BAA’ mà góc HAD + góc BAA’ = 90 0
=> góc MAD + góc ADE = 90 0 . Suy ra MA vuông góc với DE

Tam giác ABC vuông tại A
=> góc B + góc C = 90 độ
Ta có : \(\widehat{CBx}+\widehat{BCy}=90^o+90^o=180^o\)
=> \(\widehat{ABx}+\widehat{ABC}+\widehat{ACB}+\widehat{ACy}=180^o\)
\(\Rightarrow\widehat{ABx}+\widehat{ACy}+90^o=180^o\)
\(\Rightarrow\widehat{ABx}+\widehat{ACy}=90^o\)

Tam giác ABC vuông tại A
\(\Rightarrow\widehat{ABC}+\widehat{ACB}=180^o-90^o\)
\(\Rightarrow\widehat{ABC}+\widehat{ACB}=90^o\)
\(\Rightarrow\widehat{ABx}+\widehat{ABC}+\widehat{ACB}+\widehat{ACy}=90^o+35^o+55^o\)
\(\Rightarrow\widehat{CBx}+\widehat{BCy}=180^o\)\
Mà 2 góc đó ở vị trí trong cùng phía
Nên Bx // Cy