Giúp em bài cosi này vs 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Nói thật với bạn mình không biết sử dụng BĐT Cô si cho dạng này, nhưng mình có một cách làm dễ hơn, bạn tham khảo nhé.
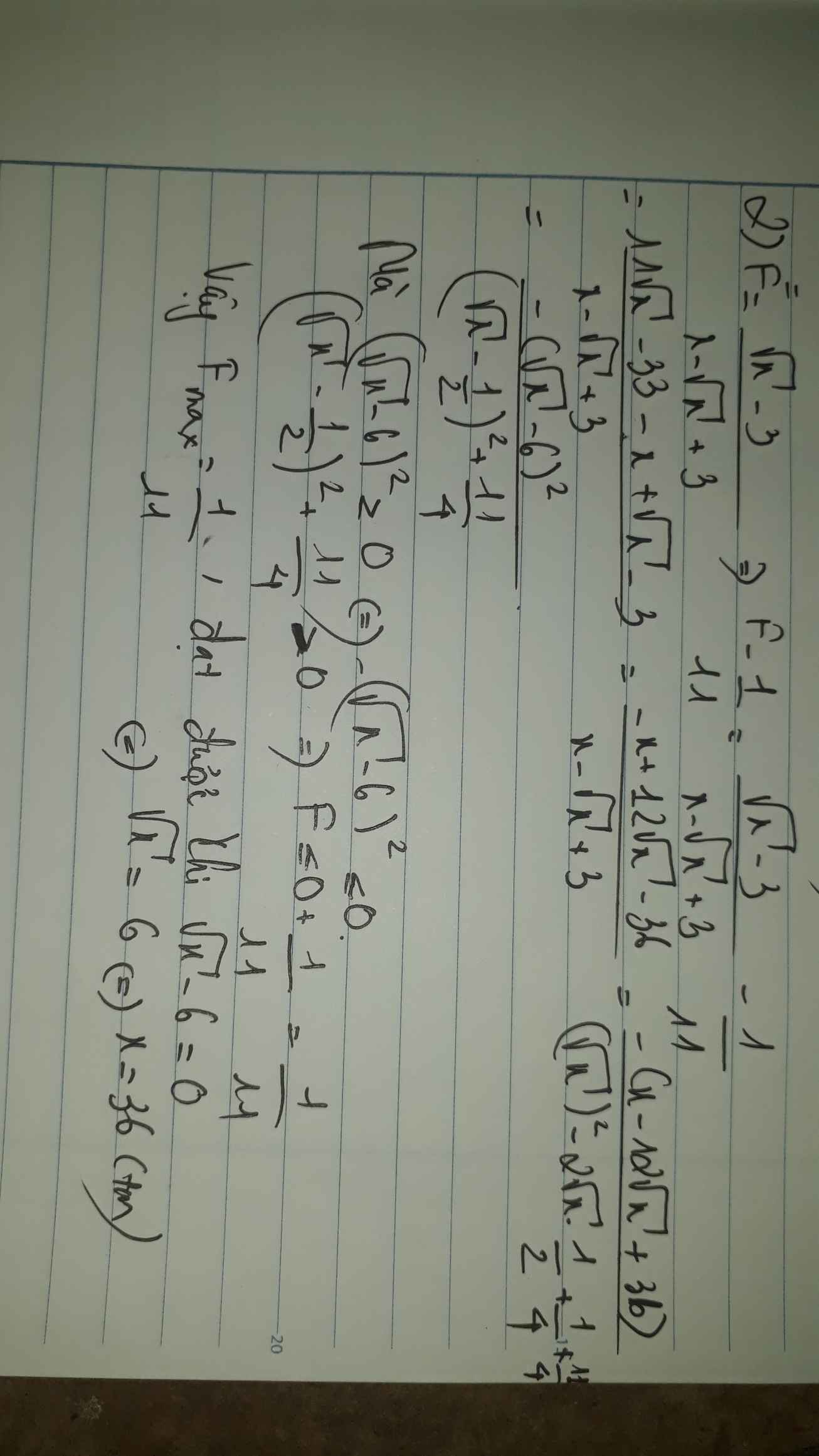
\(x>9\Rightarrow\sqrt{x}-3>0\Rightarrow F>0\)
\(\dfrac{1}{F}=\dfrac{x-\sqrt{x}+3}{\sqrt{x}-3}=\sqrt{x}+2+\dfrac{9}{\sqrt{x}-3}=\sqrt{x}-3+\dfrac{9}{\sqrt{x}-3}+5\ge2\sqrt{\dfrac{9\left(\sqrt{x}-3\right)}{\sqrt{x}-3}}+5=11\)
\(\Rightarrow F\le\dfrac{1}{11}\)
\(F_{max}=\dfrac{1}{11}\) khi \(\sqrt{x}-3=3\Rightarrow x=36\)


Để M nguyên thì \(5⋮\sqrt{a}+1\)
\(\Leftrightarrow\sqrt{a}+1\in\left\{1;5\right\}\)
\(\Leftrightarrow\sqrt{a}\in\left\{0;4\right\}\)
hay \(a\in\left\{0;16\right\}\)

Tham khảo: Cho tứ giác ABCD có góc C + góc D = 90 độ. Gọi M, N, P, Q theo thứ tự là trung điểm của AB, BD, DC, CA. Chứng minh 4 điểm M, N, P, Q cùng nằm trên 1 đường tròn - Toán học Lớp 9 - Bài tập Toán học Lớp 9 - Giải bài tập Toán học Lớp 9 | Lazi.vn - Cộng đồng Tri thức & Giáo dục


Xét ΔABD có
M là trung điểm của AB
S là trung điểm của AD
Do đó: MS là đường trung bình của ΔBAD
Suy ra: MS//BD và \(MS=\dfrac{BD}{2}\left(1\right)\)
mà BD\(\perp\)AC
nên MS\(\perp\)AC
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC
và AC\(\perp\)MS
nên MN\(\perp\)MS
Xét ΔBCD có
N là trung điểm của BC
R là trung điểm của CD
Do đó: RN là đường trung bình của ΔBCD
Suy ra: RN//BD và \(RN=\dfrac{BD}{2}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra MS//NR và MS=NR
Xét tứ giác MSRN có
MS//NR
MS=NR
Do đó: MSRN là hình bình hành
mà \(\widehat{SMN}=90^0\)
nên MSRN là hình chữ nhật
Suy ra: M,S,R,N cùng thuộc 1 đường tròn

a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.

Để A là số nguyên thì \(-5⋮2\sqrt{x}+1\)
\(\Leftrightarrow2\sqrt{x}+1\in\left\{1;5\right\}\)
\(\Leftrightarrow2\sqrt{x}\in\left\{0;4\right\}\)
hay \(x\in\left\{0;4\right\}\)

Để A là số nguyên thì \(\sqrt{x}-1⋮2\sqrt{x}+3\)
\(\Leftrightarrow2\sqrt{x}+3-5⋮2\sqrt{x}+3\)
\(\Leftrightarrow2\sqrt{x}+3=5\)
\(\Leftrightarrow\sqrt{x}=1\)
hay x=1

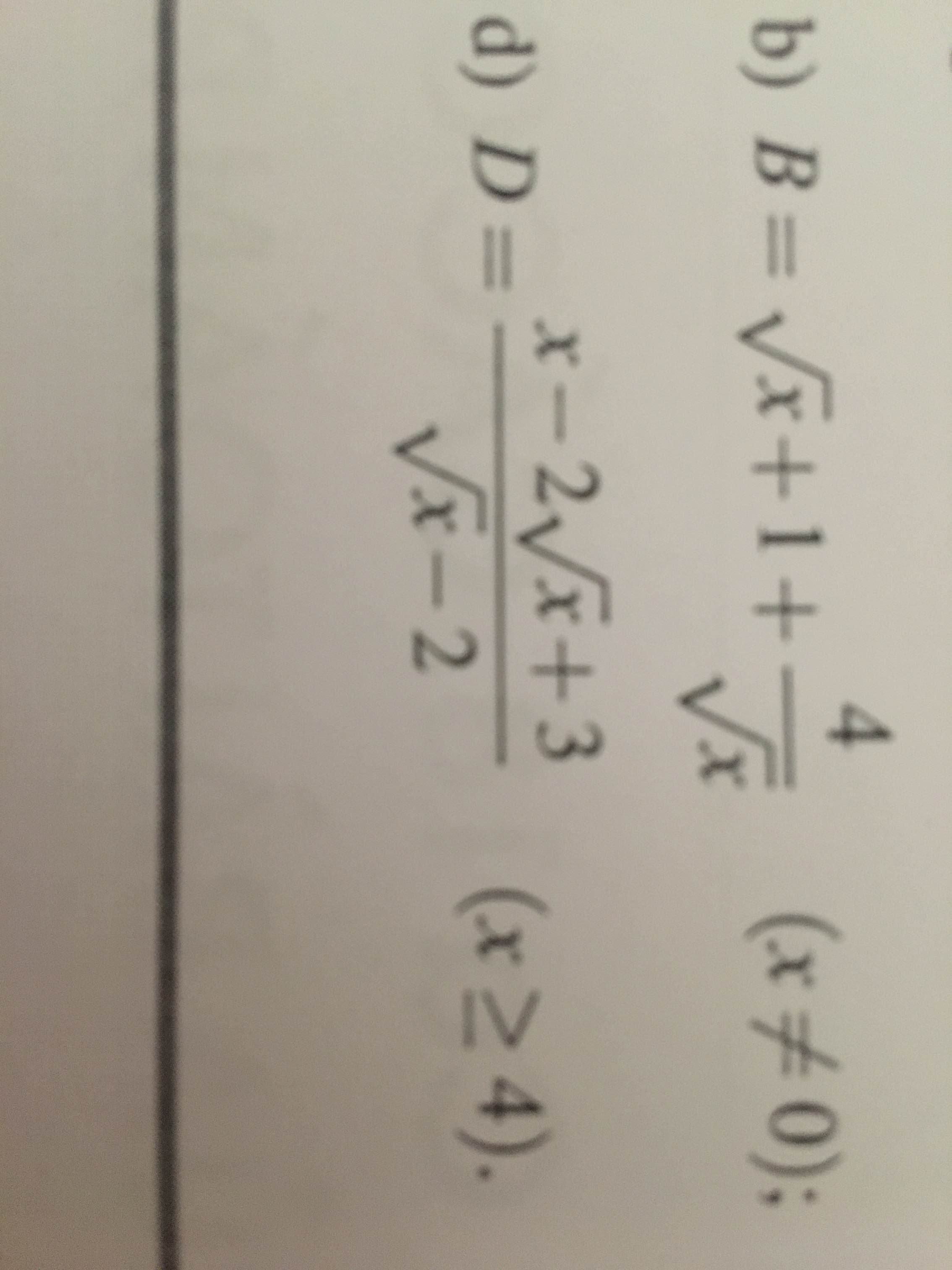
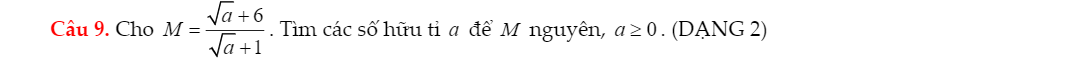
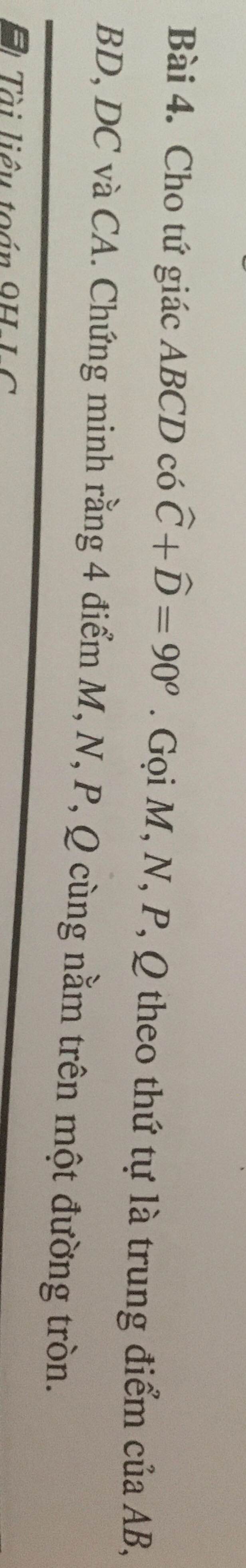


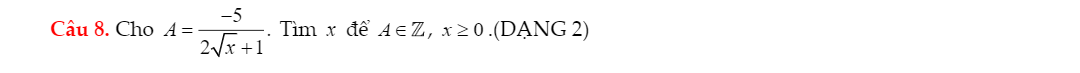

c) Ta có: \(C=\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}=\sqrt{x}+\dfrac{1}{\sqrt{x}+1}=\left(\sqrt{x}+1\right)+\dfrac{1}{\sqrt{x}+1}-1\)
Áp dụng BĐT Cô-si ta có:
\(\sqrt{x}+1+\dfrac{1}{\sqrt{x}+1}\ge2\sqrt{\left(\sqrt{x}+1\right).\dfrac{1}{\sqrt{x}+1}}=2\)
\(\Rightarrow C\ge2-1=1\)
Dấu "=" xảy ra ⇔ \(\sqrt{x}+1=1\Leftrightarrow x=0\)
a)
Ta có: \(A=\sqrt{x}-1+\dfrac{4}{\sqrt{x}-1}\ge2\sqrt{\left(\sqrt{x}-1\right).\dfrac{4}{\sqrt{x}-1}}=2\)
Dấu "=" xảy ra \(\Leftrightarrow\left(\sqrt{x}-1\right)^2=4\Leftrightarrow\sqrt{x}-1=2\Leftrightarrow x=9\)