bài 1 câu b , c nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 8:
Quyển sách đó có:
\(24:\left(1-\dfrac{1}{5}-\dfrac{2}{3}\right)=180\left(trang\right)\)
Bài 4:
a: \(A=\left(\dfrac{-5}{13}-\dfrac{21}{13}\right)+\left(\dfrac{3}{14}-\dfrac{17}{14}\right)=-2-1=-3\)
b: \(B=\dfrac{5}{4}\left(\dfrac{8}{25}+\dfrac{24}{25}-\dfrac{8}{25}\right)=\dfrac{5}{4}\cdot\dfrac{24}{25}=\dfrac{6}{5}\)
c: \(C=\dfrac{5}{9}\left(\dfrac{2}{13}+\dfrac{4}{13}+\dfrac{7}{13}\right)=\dfrac{5}{9}\cdot1=\dfrac{5}{9}\)

2b. Để A thuộc (P) thì: (2m - 1)² = 9
(2m - 1)² - 9 = 0
(2m - 1 - 3)(2m - 1 + 3) = 0
(2m - 4)(2m + 2) = 0
2m - 4 = 0 hoặc 2m + 2 = 0
*) 2m - 4 = 0
2m = 4
m = 2
*) 2m + 2 = 0
2m = -2
m = -1
Vậy m = -1; m = 2 thì A thuộc (P)

a,1/5+4/11+4/5+7/11
=(1/5+4/5)+(4/11+7/11)
=1+1
=2
Chọn B
1367.54+1367.45+1367
=1367.(54+45+1)
=1367.100
=136700


Bài 3 : Cho a . b , tính |S| biết : S=-(-a-b-c) + (-c+b+a) - (a+b)
Đề sai ,ko bao giờ đề cho a.b vì chỉ có cộng trừ thôi .Nên đề phải là a>b
Ta có: S=-(-a-b-c) + (-c+b+a) - (a+b)
S= -a+b+c-c+b+a-a-b
S= (-a+a-a)+(b+b-b)+(c-c)
S=-a+b+0
S=b-a
Mà \(a>b\Rightarrow b-a< 0\)
\(\Leftrightarrow\left|S\right|=\left|b-a\right|=a-b\)
Vậy |S|=|b-a|=a-b

b) Ta có: \(\dfrac{a}{b}=\dfrac{c}{d}\)
nên \(\dfrac{a}{c}=\dfrac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a-b}{c-d}=\dfrac{a+b}{c+d}\)
\(\Leftrightarrow\dfrac{a-b}{a+b}=\dfrac{c-d}{c+d}\)
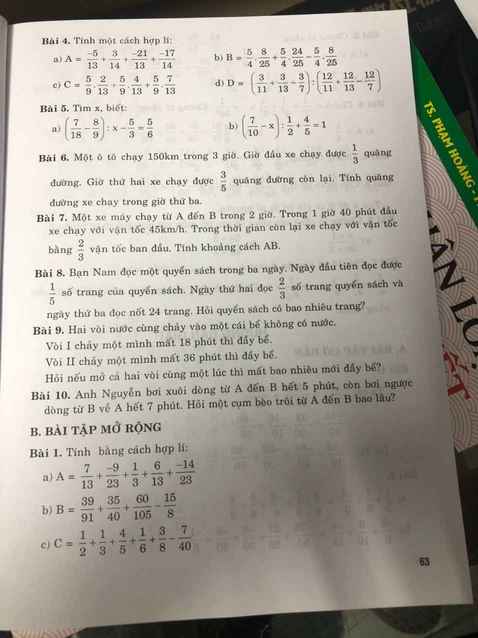


 Giúp mk bài 2 câu b, c, d nha! Vs câu BTVN nữa. Cảm on nhiều nha!
Giúp mk bài 2 câu b, c, d nha! Vs câu BTVN nữa. Cảm on nhiều nha!

Câu 1:
\(B=\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{4\sqrt{x}}{4-x}-\frac{2}{\sqrt{x}+2}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\frac{4\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\frac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\frac{x+2\sqrt{x}-4\sqrt{x}-2\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\frac{\sqrt{x}-2}{\sqrt{x}+2}\)
\(P=A.B=\left(\frac{\sqrt{x}-2}{\sqrt{x}+2}\right)^2\)
\(P< P^2\Leftrightarrow P\left(1-P\right)< 0\Leftrightarrow P>1\)(vì \(P>0\))
\(\left(\frac{\sqrt{x}-2}{\sqrt{x}+2}\right)^2>1\Leftrightarrow\orbr{\begin{cases}\frac{\sqrt{x}-2}{\sqrt{x}+2}>1\\\frac{\sqrt{x}-2}{\sqrt{x}+2}< -1\end{cases}}\Leftrightarrow\orbr{\begin{cases}\sqrt{x}-2>\sqrt{x}+2\\\sqrt{x}-2< -\sqrt{x}-2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}0\sqrt{x}>4\left(vn\right)\\\sqrt{x}< 0\left(vn\right)\end{cases}}\)
Vậy không có giá trị nào của \(x\)thỏa mãn.