Tìm x,y thuộc z biết x2-y2+2y-22=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Để giải phương trình 4x^3 + 26x^2 + 49x - y^2 + 2y + 20 = 0 và tìm các giá trị nguyên (Z) của x và y, chúng ta có thể sử dụng phương pháp đồ thị hoặc phương pháp giải đại số.
Tuy nhiên, phương trình này là một phương trình bậc ba và có cả hai biến x và y, nên việc giải phương trình này để tìm các giá trị nguyên có thể khá phức tạp và tốn nhiều thời gian.
Một phương pháp khác để tìm các giá trị nguyên của x và y là sử dụng phương pháp thử và lỗi. Bạn có thể thử từng giá trị nguyên cho x và y và kiểm tra xem liệu chúng có thỏa mãn phương trình hay không.
Nếu bạn cần tìm một số giá trị nguyên thỏa mãn phương trình, bạn có thể thử các giá trị nguyên gần nhau và sử dụng kỹ thuật giải đại số để giảm thiểu thời gian và công sức cần thiết.

\(x^2+10x+y^2-2y+26+\left(3z-6\right)^2=0\)
\(\Leftrightarrow x^2+10x+25+y^2-2y+1+\left(3z-6\right)^2=0\)
\(\Leftrightarrow\left(x+5\right)^2+\left(y-1\right)^2+\left(3z-6\right)^2=0\)
\(\Leftrightarrow\hept{\begin{cases}x+5=0\\y-1=0\\3z-6=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-5\\y=1\\z=2\end{cases}}\)

Ta có: \(\left\{{}\begin{matrix}x^2+2y+1=0\\y^2+2z+1=0\\z^2+2x+1=0\end{matrix}\right.\)
\(\Rightarrow x^2+2y+1+y^2+2z+1+z^2+2x+1=0\)
\(\Rightarrow\left(x+1\right)^2+\left(y+1\right)^2+\left(z+1\right)^2=0\)
\(\Rightarrow x=y=z=-1\)(do \(\left(x+1\right)^2,\left(y+1\right)^2,\left(z+1\right)^2\ge0\forall x,y,z\))
a) \(A=x^{2020}+y^{2020}+z^{2020}=\left(-1\right)^{2020}+\left(-1\right)^{2020}+\left(-1\right)^{2020}=1+1+1=3\)
b) \(B=\dfrac{1}{x^{2020}}+\dfrac{1}{y^{2020}}+\dfrac{1}{z^{2020}}=\dfrac{1}{\left(-1\right)^{2020}}+\dfrac{1}{\left(-1\right)^{2020}}+\dfrac{1}{\left(-1\right)^{2020}}=\dfrac{1}{1}+\dfrac{1}{1}+\dfrac{1}{1}=3\)

Lời giải:
Ta thấy:
$(-x^2y^3)^2\geq 0$ với mọi $x,y$
$(2y^2z^4=2(yz^2)^2\geq 0$ với mọi $y,z$
$\Rightarrow (2y^2z^4)^3\geq 0$ với mọi $y,z$
Do đó để tổng $(-x^2y^3)^2+(2y^2z^4)^3=0$ thì:
$-x^2y^3=2y^2z^4=0$
Hay $(x,y,z)=(x,0,z)$ với $x,z$ bất kỳ hoặc $(x,y,z)=(0,y,0)$ với $y$ là số bất kỳ.

Xin chào các bạn !!!
Hãy Đăng Kí Cho Channel Kaito1412_TV Để nhé !
Link là : https://www.youtube.com/channel/UCqgS-egZEJIX-ON873XpD_Q/videos?view_as=subscriber

Chọn A
Mặt phẳng (P) chứa đường tròn (C) (giao của 2 mặt cầu đã cho) có phương trình là: 6x + 3y + 2z = 0
Mặt phẳng (P) có phương trình là:
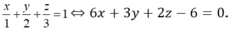
Do đó (P) // (ABC). Mặt cầu (S) tiếp xúc với cả ba đường thẳng AB, BC, CA sẽ giao với mặt phẳng (ABC) theo một đường tròn tiếp xúc với ba đường thẳng AB, BC, CA.
Trên mặt phẳng (ABC) có 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA đó là đường tròn nội tiếp tam giác ABC và ba đường tròn bàng tiếp các góc A, B, C. Do đó có 4 mặt cầu có tâm nằm trên (P) và tiếp xúc với cả ba đường thẳng AB, BC, CA. Tâm của 4 mặt cầu là hình chiếu của tâm 4 đường tròn tiếp xúc với ba đường thẳng AB, BC, CA lên mặt phẳng (P).

a) x ( x + 6 ) = 0 ⇔ x = 0 x + 6 = 0 ⇔ x = 0 x = − 6
Vậy x = 0 hoặc x = - 6
b) ( x − 3 ) . ( y + 7 ) = 0 ⇔ x − 3 = 0 y + 7 = 0 ⇔ x = 3 y = − 7
Vậy x = 3 hoặc x = -7
c) ( x − 2 ) ( x 2 + 2 ) = 0 ⇔ x − 2 = 0 x 2 + 2 = 0 ⇔ x = 2 x 2 = − 2 ( L )
Vậy x = 2
x2 - y2 + 2y - 22 = 0
<=> x2 - y2 + y + y - 1 = 21
<=> x2 - y(y - 1) + (y - 1) = 21
<=> x2 - (y + 1)(y - 1) = 21
<=> x2 - (y - 1)2 = 21
=> x2 - x(y - 1) + x(y - 1) - (y - 1)2 = 21
<=> x(x - y + 1) + (y - 1)(x - y + 1) = 21
<=> (x + y - 1)(x - y + 1) = 21
Lập bảng xét các trường hợp