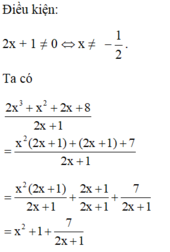Tập hợp các giá trị nguyên x để P = (2x3 - 5x2 - x + 2) : (x2 - 3x + 1) nhận giá trị nguyên là ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DV
2
19 tháng 7 2017
Ta có :
\(A=\frac{3x+5}{2+x}=\frac{3x+6-1}{2+x}=\frac{3.\left(x+2\right)-1}{2+x}=3-\frac{1}{2+x}\)
để S có giá trị nguyên thì \(\frac{1}{2+x}\in Z\)
\(\Rightarrow\)2 + x \(\in\)Ư ( 1 ) = { 1 ; -1 }
\(\Rightarrow\)x = -1 ; x = -3
khi đó : S = { -1 ; -3 }
27 tháng 9 2019
a)
Để A nguyên \(\Leftrightarrow x^3+x⋮x-1\)
\(\Leftrightarrow x^3-1+x+1⋮x-1\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)+x+1⋮x-1\left(1\right)\)
Vì x nguyên \(\Rightarrow\hept{\begin{cases}x-1\in Z\\x^2+x+1\in Z\end{cases}}\)
\(\Rightarrow\left(x-1\right)\left(x^2+x+1\right)⋮x-1\left(2\right)\)
Từ (1) và (2) \(\Rightarrow x+1⋮x-1\)
\(\Leftrightarrow x-1+2⋮x-1\)
Mà \(x-1⋮x-1\)
\(\Rightarrow2⋮x-1\)
\(\Rightarrow x-1\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
\(\Rightarrow x\in\left\{-1;0;2;3\right\}\)
Vậy \(x\in\left\{-1;0;2;3\right\}\)
27 tháng 9 2019
b) Để B nguyên \(\Leftrightarrow x^2-4x+5⋮2x-1\)
\(\Leftrightarrow2x^2-8x+10⋮2x-1\)
\(\Leftrightarrow\left(2x^2-x\right)-\left(6x-3\right)-\left(x-7\right)⋮2x-1\)
\(\Leftrightarrow x\left(2x-1\right)-3\left(2x-1\right)-\left(x-7\right)⋮2x-1\)
\(\Leftrightarrow\left(2x-1\right)\left(x-3\right)-\left(x-7\right)⋮2x-1\left(1\right)\)
Vì x nguyên \(\Rightarrow\hept{\begin{cases}2x-1\in Z\\x-3\in Z\end{cases}}\)
\(\Rightarrow\left(2x-1\right)\left(x-3\right)⋮2x-1\left(2\right)\)
Từ (1) và(2) \(\Rightarrow x-7⋮2x-1\)
\(\Leftrightarrow2x-14⋮2x-1\)
\(\Leftrightarrow2x-1-13⋮2x-1\)
Mà \(2x-1⋮2x-1\)
\(\Rightarrow13⋮2x-1\)
\(\Rightarrow2x-1\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)
Làm nốt nha các phần còn lại bạn cứ dựa bài mình mà làm
KB
8 tháng 4 2022
\(P=\dfrac{x^4+x^3-3x-1}{x^2+x+1}=\dfrac{\left(x^2-1\right)\left(x^2+x+1\right)-2x}{x^2+x+1}=x^2-1-\dfrac{2x}{x^2+x+1}\)
Vì x \(\in Z\) nên để P \(\in Z\) thì : \(\dfrac{x}{x^2+x+1}\in Z\)
Đặt \(A=\dfrac{x}{x^2+x+1}\) . Với x = 0 ; ta có : \(P=-1\in Z\)
Với x khác 0 ; ta có : \(A=\dfrac{1}{x+\dfrac{1}{x}+1}\)
Nếu x > 0 ; ta có : \(0< A\le\dfrac{1}{3}\) ( vì \(x+\dfrac{1}{x}\ge2\) ) => Ko tồn tại g/t nguyên của A (L)
Nếu x < 0 ; ta có : \(x+\dfrac{1}{x}\le-2\) \(\Rightarrow x+\dfrac{1}{x}+1\le-1\)
Suy ra : \(0>A\ge\dfrac{1}{-1}=-1\) \(\Rightarrow A=-1\)
" = " \(\Leftrightarrow x+\dfrac{1}{x}=-2\Leftrightarrow x=-1\)
x = -1 ; ta có : P = 2 \(\in Z\) (t/m)
Vậy ...
28 tháng 4 2016
2. Để A có giá trị nguyên => 11 chia hết 2n - 3
=> 2n-3 thuộc Ư(11) = { 1 ; -1 ; 11; -11}
=> 2n thuộc { 4 ; 2 ; 14 ; -8}
=> n thuộc { 2 ; 1 ; 7 ; -4}
Mà n là số tự nhiên => n = 1 ; 2; 7 (tm)
3.\(\frac{-3x-15}{-2x}=3\)=> -3x - 15 = -6x
=> -3x + 6x = 15
=> 3x = 15
=> x = 5 (tm)
4. \(\frac{2}{x+1}=\frac{x+1}{2}\)=> (x+1)2 = 4
=> (x + 1)2 = (+-2)2
=> x + 1 = +-2
=> x = 1 ; -3 (tm)
28 tháng 4 2016
Vì tích đó có chứa các thừa số 20;30;40;50;60;70;80;90 nên tích 12.14.16...96.98 có chữ số tận cùng là 0
Vậy C có chữ số tận cùng là 0
TN
1