Cho tam giác ABC vuông tại A. Gọi E là trung điểm của cạnh BC. Trên tia đối
của tia EA lấy điểm D sao cho ED = EA.
a) Chứng minh tứ giác ABDC là hình chữ nhật.
b) Gọi N là trung điểm của cạnh AC và F là điểm đối xứng của E qua N.
Chứng minh tứ giác AECF là hình thoi.
c) Gọi M là trung điểm của cạnh AB và I là trung điểm của đoạn thẳng ME.
Chứng minh ba điểm B, I, N thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABDC có
I là trung điểm của AD
I là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật

a,Xét tứ giác ABDC có:
D đối xứng với A qua M nên :
DA=DC(1)
M là trung điểm BC nên:
BM=MC(2)
Từ (1)và (2) suy ra:
tứ giác ABDC là hình chữ nhật(đpcm)
b, vì ABDC là hình chữ nhật nên:
AB=DC và AB//DC
mà DC=FC và F trên tia DC
=>AB=FC và AB//FC
vậy tứ giác ABCF là hình bình hành(đpcm)

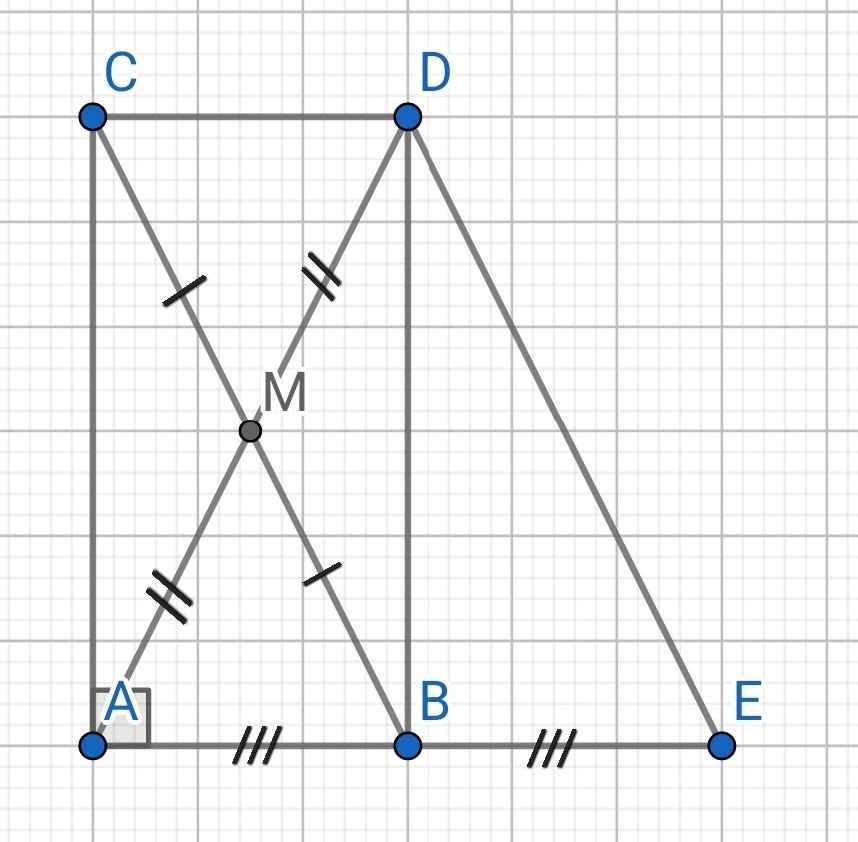 a) Tứ giác ABDC có:
a) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật (cmt)
⇒ CD = AB (1)
Do B là trung điểm của AE (gt)
⇒ BE = AB = AE : 2 (2)
Từ (1) và (2) ⇒ CD = BE
Do ABDC là hình chữ nhật (cmt)
⇒ CD // AB
⇒ CD // BE
Tứ giác BEDC có:
CD // BE (cmt)
CD = BE (cmt)
⇒ BEDC là hình bình hành
c) Do ABDC là hình chữ nhật (cmt)
⇒ AC // BD
Do đó AC, BD, EK đồng quy là vô lý
Em xem lại đề nhé!

Xét tứ giác ABDC có
O là trung điểm của BC
O là trung điểm của AD
Do đó: ABDC là hình bình hành

a: Xét ΔABC có
M là trung điểm của AC
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AB
hay AMNB là hình thang
mà \(\widehat{MAB}=90^0\)
nên AMNB là hình thang vuông

a) Xét ∆CMA và ∆BMD:
Góc CMA= góc BMD (đối đỉnh)
MA=MD (gt)
MC=MB (M là trung điểm BC)
=> ∆CMA=∆BMD(c.g.c)
=> góc CAM = góc BDM và CA=DB
Mà 2 góc CAM và góc BDM nằm ở vị trí so lo trong nên CA//DB
=> CABD là hình bình hành
Lại có góc CAB = 90 độ (gt)
=> ACDB là hình chữ nhật
b) Vì E là điểm đối xứng của C qua A nên EAB=90độ=DBA
Mà 2 góc này ở bị trí so le trong nên AE//DB
Lại có AE=BD(=CA)
=> AEBD là hình bình hành

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{EAD}=90^0\)
Do đó: ADME là hình chữ nhật

a: Xét tứ giác AHBD có
M là trung điểm của AB
M là trung điểm của HD
Do đó: AHBD là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBD là hình chữ nhật
b: Xét ΔAEB có
H là trung điểm của EB
M là trung điểm của AB
Do đó: HM là đường trung bình
=>HM//AE và HM=AE/2
hay HD//AE và HD=AE
hay ADHE là hình bình hành


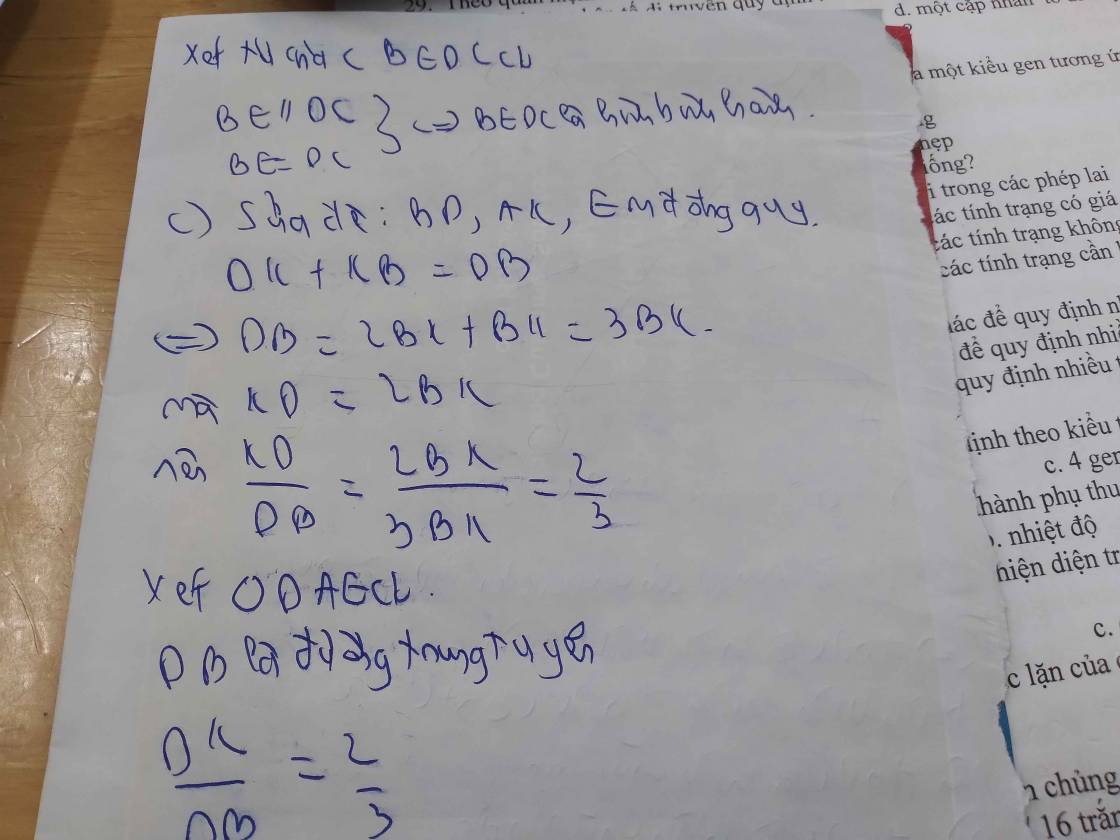

a: Xét tứ giác ABDC có
E là trung điểm của đường chéo BC
E là trung điểm của đường chéo AD
Do đó: ABDC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABDC là hình chữ nhật
b: Ta có: ΔABC vuông tại A
mà AE là đường trung tuyến ứng với cạnh huyền BC
nên AE=BE=CE
Xét tứ giác AECF có
N là trung điểm của đường chéo FE
N là trung điểm của đường chéo AC
Do đó: AECF là hình bình hành
mà AE=CE
nên AECF là hình thoi