Bài 2 Từ 1 điểm M ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy một điểm C. Vẽ CD, CE, CF lầm lượt vuông góc với AB, MA, MB . Gọi I là giao đieme của AC và DE , K là giao điểm của BC và DF. Chứng minh rằng:
a: các tứ giác AECD , BFCD nội tiếp
b: CD2 =CE× CF
c: tứ giác ICKD nội...
Đọc tiếp
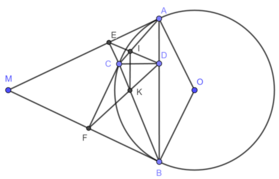
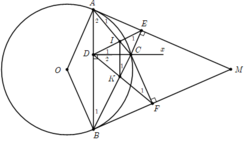
Bài 2 Từ 1 điểm M ở bên ngoài đường tròn (O) ta vẽ hai tiếp tuyến MA, MB với đường tròn. Trên cung nhỏ AB lấy một điểm C. Vẽ CD, CE, CF lầm lượt vuông góc với AB, MA, MB . Gọi I là giao đieme của AC và DE , K là giao điểm của BC và DF. Chứng minh rằng:
a: các tứ giác AECD , BFCD nội tiếp
b: CD2 =CE× CF
c: tứ giác ICKD nội tiếp
Lời giải:
a)
\(CD\perp AB, CE\perp AM, CF\perp MB\Rightarrow \left\{\begin{matrix} \widehat{CDA}=\widehat{CEA}=90^0\\ \widehat{CFB}=\widehat{CDB}=90^0\end{matrix}\right.\)
\(\Rightarrow \left\{\begin{matrix} \widehat{CDA}+\widehat{CEA}=180^0\\ \widehat{CFB}+\widehat{CDB}=180^0\end{matrix}\right.\)
Tứ giác $AECD$ và $BFCD$ có tổng hai góc đối bằng $180^0$ nên là tứ giác nội tiếp.
b)
Từ kết quả 2 tứ giác nội tiếp trên, kết hợp với tính chất góc tạo bởi tiếp tuyến và dây cung thì bằng góc nội tiếp chắn dây cung đó ta có:
\(\widehat{CDF}=\widehat{CBF}=\widehat{CAB}=\widehat{CAD}=\widehat{CED}\)
\(\widehat{CFD}=\widehat{CBD}=\widehat{CBA}=\widehat{EAC}=\widehat{CDE}\)
Do đó \(\triangle CDF\sim \triangle CED(g.g)\)
\(\Rightarrow \frac{CD}{CF}=\frac{CE}{CD}\Rightarrow CD^2=CE.CF\)
c)
Theo phần b:
\(\widehat{IDK}=\widehat{CDF}+\widehat{CDE}=\widehat{EAC}+\widehat{FBC}\)
\(=\widehat{CBA}+\widehat{CAB}=180^0-\widehat{ACB}=180^0-\widehat{ICK}\)
\(\Rightarrow \widehat{IDK}+\widehat{ICK}=180^0\)
Do đó tứ giác $ICKD$ nội tiếp.