Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét ΔABC có
F là trung điểm của AB
H là trung điểm của BC
Do đó: FH là đường trung bình của ΔABC
Suy ra: FH//AC
hay AFHC là hình thang
a: Xét ΔADC và ΔAEB có
AD=AE
góc DAC chung
AC=AB
=>ΔADC=ΔAEB
b: AD+DB=AB
AE+EC=AC
mà AB=AC và AD=AE
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
góc DBC=góc ECB
BC chung
=>ΔDBC=ΔECB
=>góc KBC=góc KCB
=>ΔKBC cân tại K
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
DO đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
Ta có: DE=DB+BC+CE
nên DE=AB+BC+AC=CABC
- Ai đó giúp tớ giải bài toán này với :v Tớ cảm ơn nhiều nhiều nhiều lắm luôn ý!
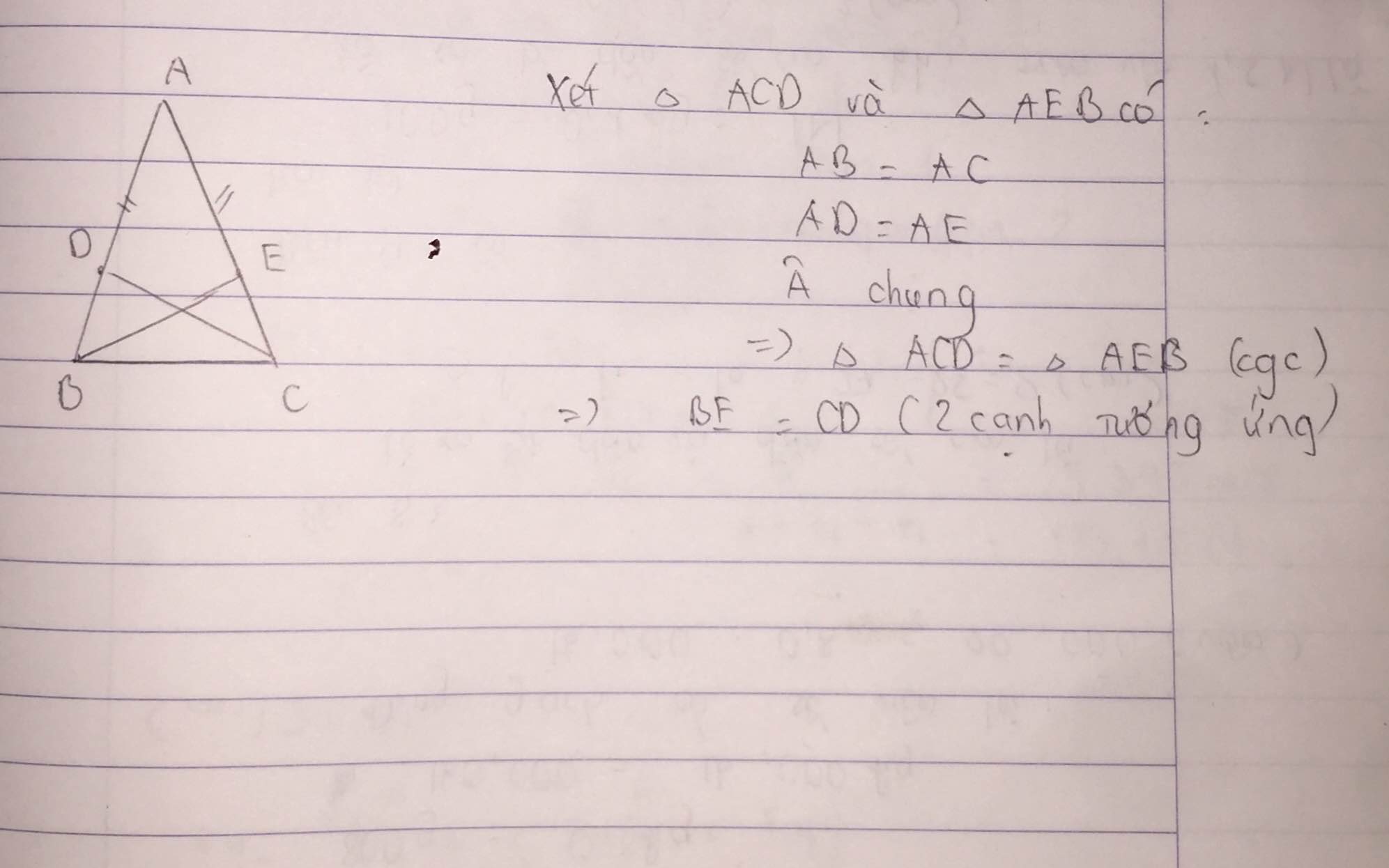
a: Xét ΔABD và ΔACE có
AB=AC
góc BAD chung
AD=AE
Do đó: ΔABD=ΔACE
Suy ra: góc ABD=góc ACE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=DB
Do đó: ΔEBC=ΔDCB
Suy ra: góc IBC=góc ICB
hay ΔIBC cân tại I
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
d: Ta có: IB=IC
nênI nằm trên đườg trung trực của BC(1)
Ta có: ΔABC cân tại A
mà AH là đường cao
nen AH là đường trung trực của BC(2)
Từ (1) và (2) suy ra A,I,H thẳng hàng