Cho hình bình hành ABCD (AC > BD). Gọi E, F lần lượt là hình chiếu của C lên các đường thẳng AB, AD. Chứng minh rằng:
a) AB.AE + AD.AF = AC2
b) \(\Delta FCE\sim\Delta ABC\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HA
11 tháng 6 2021
a, Xét ΔAHD và ΔAFC có:
ˆAHD= ˆAFC=90 độ
ˆA chung
⇒ΔAHD và ΔAFC đồng dạng (g,g)
⇒AH/AF=AD/AC=AD/AC⇒AD.AF=AC.AH
b,
Từ B kẻ BK⊥AC
Chứng minh tương tự như trên ta có:
AB.AE=AK.AC
Mà AK=HC (tam giác ABK và tam giác CDH bằng nhau)
⇒AD.AF+AB.AE=AC.AH+AK.AC=AC(AH+AK)=AC(AH+HC)=AC.AC=AC^2
24 tháng 6 2021
1) Có \(\widehat{ABC}=\widehat{ADC}\)
\(\Rightarrow180^0-\widehat{ABC}=180^0-\widehat{ADC}\) \(\Leftrightarrow\widehat{EBC}=\widehat{CDF}\)
Xét \(\Delta BCE\) và \(\Delta DCF\) có:
\(\Leftrightarrow\widehat{EBC}=\widehat{CDF}\)
\(\widehat{E}=\widehat{F}=90^0\)
nên \(\Delta BCE\sim\Delta DCF\left(g.g\right)\) \(\Rightarrow\dfrac{CE}{CF}=\dfrac{CB}{CD}\) \(\Leftrightarrow CE.CD=CF.CB\)
Có \(\widehat{EAF}+\widehat{ECF}=360^0-\widehat{AEC}-\widehat{AFC}=360^0-90^0-90^0=180^0\)
mà \(\widehat{BAD}+\widehat{ABC}=180^0\) (hai góc so le trong do BC//AD)
\(\Rightarrow\widehat{ECF}=\widehat{ABC}\) (1)
mà \(CE.CD=CB.CF\) (cm trên)\(\Leftrightarrow CE.AB=CB.CF\) \(\Leftrightarrow\dfrac{CE}{CB}=\dfrac{CF}{AB}\) (2)
Từ (1);(2) \(\Rightarrow\Delta ABC\sim\Delta FCE\left(c.g.c\right)\)
2. Kẻ \(DK\perp AC\) tại K
Dễ chững minh được \(\Delta ADK\sim ACF\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AC}=\dfrac{AK}{AF}\Leftrightarrow AD.AF=AC.AK\) (*)
Dễ chứng minh được \(\Delta CDK\sim\Delta ACE\left(g.g\right)\)
\(\Rightarrow\dfrac{CK}{AE}=\dfrac{CD}{AC}\Leftrightarrow CK.AC=AE.CD\) mà DC=AB
\(\Rightarrow AB.AE=CK.AC\) (3*)
Từ (*);(2*) cộng vế với vế \(\Rightarrow AB.AE+AD.AF=AC.CK+AC.AK=AC\left(CK+AK\right)\)
\(\Rightarrow AB.AE+AD.AF=AC^2\)
Vậy...
CM
3 tháng 7 2018
Dựng BG ⊥ AC.
Xét ΔBGA và ΔCEA, ta có:
∠ (BGA) = ∠ (CEA) = 90 0
∠ A chung
⇒ △ BGA đồng dạng △ CEA(g.g)
Suy ra: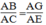 
AB.AE = AC.AG (1)
Xét △ BGC và △ CFA, ta có:
∠ (BGC) = ∠ (CFA) = 90 0
∠ (BCG) = ∠ (CAF) (so le trong vì AD //BC)
△ BGC đồng dạng △ CFA (g.g)
Suy ra: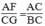 
⇒ BC.AF = AC.CG
Mà BC = AD (tính chất hình bình hành)
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
AB.AE + AD.AF= AC(AG + CG)
Mà AG + CG = AC nên AB.AE + AD.AF = A C 2