Hộ mình với ạ
Giải các phương trình trùng phương : a, 4x4+x2-5=0
b, 3x4+4x2+1=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 4 2019
a) 4 x 4 + x 2 − 5 = 0
Đặt x 2 = t (t ≥ 0). Phương trình trở thành:
4 t 2 + t − 5 = 0
Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm
t 1 = 1 ; t 2 = ( − 5 ) / 4
Do t ≥ 0 nên t = 1 thỏa mãn điều kiện
Với t = 1, ta có: x 2 = 1 ⇔ x = ± 1
Vậy phương trình có 2 nghiệm x 1 = 1 ; x 2 = − 1
b) 3 x 4 + 4 x 2 + 1 = 0
Đặt x 2 = t ( t ≥ 0 ) . Phương trình trở thành:
3 t 2 + 4 t + 1 = 0
Nhận thấy phương trình có dạng a - b + c = 0 nên phương trình có nghiệm
t 1 = - 1 ; t 2 = ( - 1 ) / 3
Cả 2 nghiệm của phương trình đều không thỏa mãn điều kiện t ≥ 0
Vậy phương trình đã cho vô nghiệm.
PT
1
CM
7 tháng 11 2019
3x4 + 4x2 + 1 = 0
Đặt x2 = t (t ≥ 0). Phương trình trở thành:
3t2 + 4t + 1 = 0
Nhận thấy phương trình có dạng a - b + c = 0 nên phương trình có nghiệm
t1 = -1; t2 = (-1)/3
Cả 2 nghiệm của phương trình đều không thỏa mãn điều kiện t ≥ 0
Vậy phương trình đã cho vô nghiệm.
PT
1
CM
14 tháng 9 2019
4x4 + x2 – 5 = 0;
Đặt x2 = t (t ≥ 0). Phương trình trở thành:
4t2 + t - 5 = 0
Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm
t1 = 1; t2 =(-5)/4
Do t ≥ 0 nên t = 1 thỏa mãn điều kiện
Với t = 1, ta có: x2 = 1 ⇔ x = ±1
Vậy phương trình có 2 nghiệm x1 = 1; x2 = -1
PT
1
CM
25 tháng 2 2017
3x4 + 10x2 + 3 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : 3t2 + 10t + 3 = 0 (2)
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ’ = 52 – 3.3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
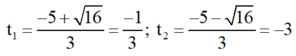
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
PT
1
CM
23 tháng 7 2019
a) x 4 – 5 x 2 + 4 = 0 ( 1 )
Đặt x 2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t 2 – 5 t + 4 = 0 ( 2 )
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t 1 = 1 ; t 2 = c / a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x 2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) 2 x 4 – 3 x 2 – 2 = 0 ; ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 2 t 2 – 3 t – 2 = 0 ( 2 )
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = ( - 3 ) 2 - 4 . 2 . ( - 2 ) = 25 > 0
⇒ Phương trình có hai nghiệm
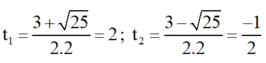
Chỉ có giá trị t 1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
c) 3 x 4 + 10 x 2 + 3 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 3 t 2 + 10 t + 3 = 0 ( 2 )
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ ’ = 5 2 – 3 . 3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
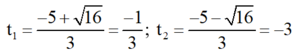
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
bạn chỉ cần gọi x\(^2\)=t(t\(\ge\)0)
ta có p/trình mới có dạng: a.t\(^2\)+b.t+c=0
giải phương trình bậc hai theo cách tính \(\Delta\)=b\(^2\)-4.a.c và xét dấu\(\Delta\)
Nếu delta nhỏ hơn 0 => pt vô nghiệm => ko tìm đc t=> ko tìm đc x
Nếu delta bằng 0 => pt có nghiệm kép t\(_1\)=t\(_2\)=\(\dfrac{-b}{2a}\)(xét điều kiện của t)=> thay t=\(\dfrac{-b}{2a}\)vào x\(^2\)=t ta tính đc: x=\(\sqrt{\dfrac{-b}{2a}}\)
Nếu delta lớn hơn 0 => pt có 2 nghiệm phân biệt t\(_1\)= \(\dfrac{-b+\sqrt{\Delta}}{2a}\)
t\(_2\)=\(\dfrac{-b-\sqrt{\Delta}}{2a}\)
thay từng TH của t vào x\(^2\)=t tìm x và kết luận.
Chúc bạn hoc tốt!