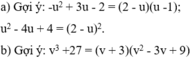Cho u \(\le\) v . Chứng minh rằng : u3 - 3u \(\le\) v3 - 3v + 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :
<=> u3 - 3u - 2 \(\le\) v3 - 3v + 2 <=> ( u + 1 )2( u - 2 ) \(\le\) ( v - 1 )2( v + 2 )
Đặt x = u + 1 , y = v -1 thì :
BĐT <=> x3 - 3x2 \(\le\) y3 + 3y2 <=> x3 - y3 \(\le\) 3(x2 + y2)
Ta có : x - y = ( u - v ) + 2 \(\le\)2
=> ( x - y ) ( x2 + xy + y2 ) \(\le\)2( x2 + xy + y2) = 2(x2 + y2) + 2xy \(\le\) 2(x2 + y2) + ( x2 + y2 ) = 3(x2 + y2 ) => x3 - y3 \(\le\) 3(x2 +y2 ) ( đpcm)
Dấu bằng xảy ra khi <=> x = y = 0 <=> u = -1 ; v = 1

Do \(-1\le a;b;c\le1\)
\(\Rightarrow\left(1-a\right)\left(1-b\right)\left(1-c\right)+\left(1+a\right)\left(1+b\right)\left(1+c\right)\ge0\)
\(\Leftrightarrow1-abc-a-b-c+ab+bc+ca+1+abc+b+c+c+ab+bc+ca\ge0\)
\(\Leftrightarrow2\left(ab+bc+ca\right)+2\ge0\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)+2\ge a^2+b^2+c^2\)
\(\Leftrightarrow\left(a+b+c\right)^2+2\ge a^2+b^2+c^2\)
\(\Leftrightarrow a^2+b^2+c^2\le2\)
Mà \(\left|a\right|;\left|b\right|;\left|c\right|\le1\Rightarrow\left\{{}\begin{matrix}a^4\le a^2\\b^6\le b^2\\c^8\le c^2\end{matrix}\right.\)
\(\Rightarrow a^4+b^6+c^8\le a^2+b^2+c^2\le2\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(-1;0;1\right)\) và các hoán vị

Thực hiện phép nhân đa thức với đa thức ở vế trái
a) VT = 3 u 2 + 9u + 27 – ( u 3 – 32 u 2 + 9u) = 27 – u 3 = VP (đpcm).
b) VT = ( t 2 – 4)( t 2 + 4) = t 4 – 16 = VP. (đpcm).

Từ a+b+c=6 \(\Rightarrow\)a+b=6-c
Ta có: ab+bc+ac=9\(\Leftrightarrow\)ab+c(a+b)=9
\(\Leftrightarrow\)ab=9-c(a+b)
Mà a+b=6-c (cmt)
\(\Rightarrow\)ab=9-c(6-c)
\(\Rightarrow\)ab=9-6c+c2
Ta có: (b-a)2\(\ge\)0 \(\forall\)b, c
\(\Rightarrow\)b2+a2-2ab\(\ge\)0
\(\Rightarrow\)(b+a)2-4ab\(\ge\)0
\(\Rightarrow\)(a+b)2\(\ge\)4ab
Mà a+b=6-c (cmt)
ab= 9-6c+c2 (cmt)
\(\Rightarrow\)(6-c)2\(\ge\)4(9-6c+c2)
\(\Rightarrow\)36+c2-12c\(\ge\)36-24c+4c2
\(\Rightarrow\)36+c2-12c-36+24c-4c2\(\ge\)0
\(\Rightarrow\)-3c2+12c\(\ge\)0
\(\Rightarrow\)3c2-12c\(\le\)0
\(\Rightarrow\)3c(c-4)\(\le\)0
\(\Rightarrow\)c(c-4)\(\le\)0
\(\Rightarrow\hept{\begin{cases}c\ge0\\c-4\le0\end{cases}}\)hoặc\(\hept{\begin{cases}c\le0\\c-4\ge0\end{cases}}\)
*\(\hept{\begin{cases}c\ge0\\c-4\le0\end{cases}\Leftrightarrow\hept{\begin{cases}c\ge0\\c\le4\end{cases}\Leftrightarrow}0\le c\le4}\)
*

\(VT\le\frac{x^2+16-y}{2}+\frac{y+16-x^2}{2}=\frac{32}{2}=16\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x\ge0\\y=16-x^2\end{matrix}\right.\)

Đề bài không rõ ràng. n ở đây là tự nhiên, nguyên hay là chơi luôn cả R