cho 4 đường thẳng phân biệt a;b;c;d.Hỏi 4 đường thẳng đó cắt nhau tại bao nhiêu điểm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
Cách 1:
TH1: 2 điểm thuộc a và 1 điểm thuộc b
Số cách chọn 2 điểm thuộc đường thẳng a là \(C_3^2\) (cách chọn)
Số cách chọn 1 điểm thuộc đường thẳng b là: \(C_4^1\) (cách chọn)
=> Số tam giác tạo thành là: \(C_3^2 . C_4^1 = 12\)
TH2: 2 điểm thuộc b và 1 điểm thuộc a
Số cách chọn 2 điểm thuộc đường thẳng b là \(C_4^2\) (cách chọn)
Số cách chọn 1 điểm thuộc đường thẳng a là: \(C_3^1\) (cách chọn)
=> Số tam giác tạo thành là: \(C_4^2 + C_3^1 = 18\)
Vậy có tất cả 12 + 18 = 30 tam giác.
Cách 2:
Số cách chọn 3 điểm thuộc đường thẳng a là: \(C_3^3\) (cách chọn)
Số cách chọn 3 điểm thuộc đường thẳng b là: \(C_4^3\) (cách chọn)
Số cách chọn 3 điểm bất kì trong 7 điểm đã cho là: \(C_7^3\) (cách chọn)
Số cách chọn 3 điểm không thẳng hàng trong 7 điểm đã cho là: \(C_7^3 - C_4^3 - C_3^3 = 30\) (cách chọn)
Vậy số tam giác có thể có là : 30 (tam giác)
CM
12 tháng 7 2019
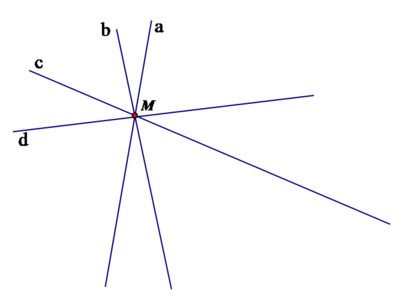
Gọi M là một điểm chung mà 3 đường thẳng a, b, c đi qua. Do đó, 2 đường thẳng b và c cắt nhau tại M. Mà 3 đường thẳng b, c, d có 1 điểm chung nên đường thẳng d cũng đi qua M. Vậy 4 đường thẳng a, b, c, d cắt nhau tại 1 điểm.
TT
2
18 tháng 10 2015
Lấy 1 điểm trong số 4 điểm đó nối với 3 điểm còn lại ta được 3 giao điểm.
=>Có 4 điểm nối được:
3.4=12(giao điểm)
Vì mỗi giao điểm được tính 2 lần
=>Có số giao điểm là:
12:2=6(giao điểm)
LC
18 tháng 10 2015
Lấy 1 điểm trong số 4 điểm đó nối với 3 điểm còn lại ta được 3 giao điểm.
=>Có 4 điểm nối được:
3.4=12(giao điểm)
Vì mỗi giao điểm được tính 2 lần
=>Có số giao điểm là:
12:2=6(giao điểm)
27 tháng 3 2016
( Tớ giải bài 2 thôi nhé! )
Nếu số cần tìm trừ đi 4 thì số mới chia hết cho cả 5 ; 6 và 7.
Mà BCNN { 5 ; 6 ; 7 } = 210 ( do lớn hơn 4 )
Vậy số cần tìm là: 210 + 4 = 214
Đáp số: 214