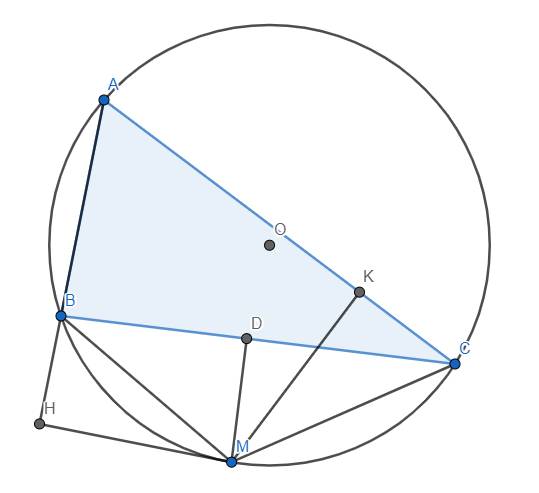
Cho tam giác ABC có ba góc nhọn, nội tiếp trong một đường tròn. Lấy điểm D trên cung BC (không chứa điểm A) của đường tròn đó. Gọi H,K,I lần lượt là chân đường vuông góc hạ từ D xuống các đường thẳng BC,AB, AC.
a. Chứng minh ba điểm K,H,I thẳng hàng
b. Chứng minh: \(\dfrac{BC}{DH}\)=\(\dfrac{AC}{DI}\)+\(\dfrac{AB}{DK}\)