Tính tích \(\dfrac{1}{2}.\dfrac{1}{4}.\dfrac{1}{6}....\dfrac{1}{n}\)
(Dùng lệnh While Do)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 3 2021
Bài 1:
uses crt;
var a:real;
i,n:integer;
begin
clrscr;
write('Nhap n='); readln(n);
a:=0;
i:=1;
while i<=n do
begin
a:=a+1/i;
i:=i+1;
end;
writeln(a:4:2);
readln;
end.
1 tháng 3 2018
Var i , n : integer;
S: real;
Begin
write (' n ='); read (n);
S:= 0
For i:= 1 to n do S:= S+ 1/i;
Write (S);
Readln;
End.
3 tháng 4 2018
program bai1;
var s,n,i:longint;
begin
write('N= ');readln(n);
s:=0;
for i:=1 to n do s:=s+1/i;
write('s= ',s);
readln
end.
27 tháng 2 2018
Var i , n : Integer;
S : real;
Begin
write (' n = ') ; read (n);
S:=0
For i:=1 to n do S:= S + 1/i;
Writeln ( S );
Readln;
End.
3 tháng 4 2018
program bai1;
var i,n,s:longint;
begin
write('N= ');
readln(n);
s:=1;
for i:=2 to n do s:=s+1/i;
write('s= ',s);
readln
end.
22 tháng 2 2022
a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: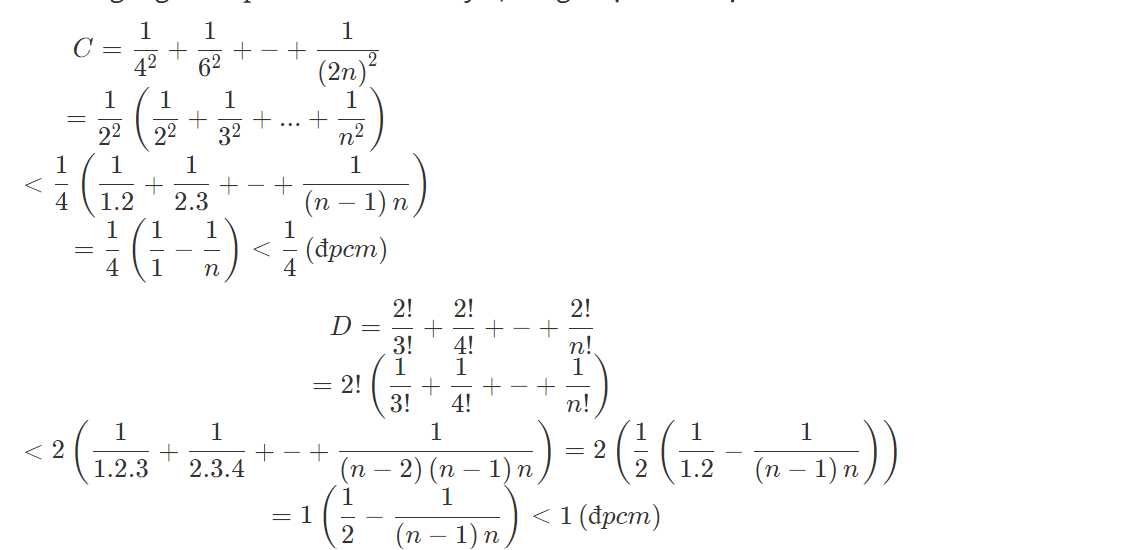 
2 tháng 7 2021
Ta có: \(M=\dfrac{\dfrac{1}{99}+\dfrac{2}{98}+\dfrac{3}{97}+\dfrac{4}{96}+...+\dfrac{97}{3}+\dfrac{98}{2}+\dfrac{99}{1}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{100}}\)
\(=\dfrac{\left(1+\dfrac{1}{99}\right)+\left(1+\dfrac{2}{98}\right)+\left(1+\dfrac{3}{97}\right)+\left(1+\dfrac{4}{96}\right)+...+\left(1+\dfrac{98}{2}\right)+1}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{100}}\)
\(=\dfrac{\dfrac{100}{99}+\dfrac{100}{98}+\dfrac{100}{97}+...+\dfrac{100}{1}+\dfrac{100}{2}}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+...+\dfrac{1}{100}}\)
=100
Ta có: \(N=\dfrac{92-\dfrac{1}{9}-\dfrac{2}{10}-\dfrac{3}{11}-...-\dfrac{90}{98}-\dfrac{91}{99}-\dfrac{92}{100}}{\dfrac{1}{45}+\dfrac{1}{50}+\dfrac{1}{55}+...+\dfrac{1}{495}+\dfrac{1}{500}}\)
\(=\dfrac{\left(1-\dfrac{1}{9}\right)+\left(1-\dfrac{2}{10}\right)+\left(1-\dfrac{3}{11}\right)+...+\left(1-\dfrac{90}{98}\right)+\left(1-\dfrac{91}{99}\right)+\left(1-\dfrac{92}{100}\right)}{\dfrac{1}{5}\left(\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{99}+\dfrac{1}{100}\right)}\)
\(=\dfrac{\dfrac{8}{9}+\dfrac{8}{10}+\dfrac{8}{11}+...+\dfrac{8}{99}+\dfrac{8}{100}}{\dfrac{1}{5}\left(\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{99}+\dfrac{1}{100}\right)}\)
\(=\dfrac{8}{\dfrac{1}{5}}=40\)
\(\Leftrightarrow\dfrac{M}{N}=\dfrac{100}{40}=\dfrac{5}{2}\)
GL
24 tháng 8 2023
a) \(1+\dfrac{4}{9}=\dfrac{9}{9}+\dfrac{4}{9}=\dfrac{9+4}{9}=\dfrac{13}{9}\)
b) \(5+\dfrac{1}{2}=\dfrac{10}{2}+\dfrac{1}{2}=\dfrac{10+1}{2}=\dfrac{11}{2}\)
c) \(3-\dfrac{5}{6}=\dfrac{18}{6}-\dfrac{5}{6}=\dfrac{18-5}{6}=\dfrac{13}{6}\)
d) \(\dfrac{31}{7}-2=\dfrac{31}{7}-\dfrac{14}{7}=\dfrac{31-14}{7}=\dfrac{17}{7}\)
CC
3 tháng 10 2018
\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{8}-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{7}\)
\(\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}+\dfrac{1}{3}\right)+\left(\dfrac{1}{4}-\dfrac{1}{4}\right)+\left(-\dfrac{1}{5}+\dfrac{1}{5}\right)+\left(\dfrac{1}{6}-\dfrac{1}{6}\right)+\left(\dfrac{-1}{7}+\dfrac{1}{7}\right)+\dfrac{1}{8}\)
=0+0+0+0+0+0+\(\dfrac{1}{8}\)
=\(\dfrac{1}{8}\)
BD
18 tháng 8 2023
\(\dfrac{1}{2}-\dfrac{2}{3}+\dfrac{3}{4}-\dfrac{4}{5}+\dfrac{5}{6}-\dfrac{6}{7}-\dfrac{6}{5}+\dfrac{4}{5}-\dfrac{3}{4}+\dfrac{2}{3}-\dfrac{1}{2}\)
\(=\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+\left(-\dfrac{2}{3}+\dfrac{2}{3}\right)+\left(\dfrac{3}{4}-\dfrac{3}{4}\right)+\left(-\dfrac{4}{5}+\dfrac{4}{5}\right)+\left(\dfrac{5}{6}-\dfrac{6}{7}-\dfrac{6}{5}\right)\)
\(=0+0+0+0-\dfrac{257}{210}\)
\(=\dfrac{257}{210}\)
program bai1;
var s,i,n:longint;
begin
write('N= '):readln(n);
i:=0;
s:=1;
while i<=n do
begin
if i mod 2=0 then s:=s*1/i;
i:=i+1;
end;
write('S= ',s);
readln
end.
Var i,n:integer;
S:real;
Begin
Write (' nhap n : ');
Readln(n);
S:=1;
While i<=n do S:=S*1/i;
Write (' tong S : ',S:5:6);
Readln;
end.