bài 1: một xe chuyển động từ A về B. Trong quãng đường đầu, xe chuyển động với vận tốc v1 = 27km/h trong 20 phút. Trong 2/3 quãng đường còn lại xe chuyển động với vận tốc v2. Biết vtb của xe trên cả quãng đường AB là V=54km/h. Tính v2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 9 2021
\(v_1=27\left(\dfrac{km}{h}\right)\\ s_1=27.\dfrac{1}{3}=9\left(km\right)\\ v_{tb}=54\left(\dfrac{km}{h}\right)\\ s_{AB}=9:\left(1-\dfrac{2}{3}\right)=27\left(km\right)\\ v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{27}{\dfrac{1}{3}+\dfrac{s_2}{v_2}}\\ \Leftrightarrow54=\dfrac{27}{\dfrac{1}{3}+\dfrac{27-9}{v_2}}\\ \Leftrightarrow v_2=108\left(\dfrac{km}{h}\right)\)
TK
28 tháng 8 2021
Vận tốc trung bình của xe trên quãng đường còn lại là
\(v'=\dfrac{t\left(\dfrac{2v_2}{3}+\dfrac{v_3}{3}\right)}{t}=\dfrac{1\left(\dfrac{2\cdot50}{3}+\dfrac{40}{3}\right)}{1}=\dfrac{140}{3}\left(\dfrac{km}{h}\right)\)
Vận tốc trung bình trên cả quảng đường là
\(v=\dfrac{s}{s\left(\dfrac{1}{3v_1}+\dfrac{2}{3v'}\right)}=\dfrac{1}{1\left(\dfrac{1}{3\cdot60}+\dfrac{2}{3\cdot\dfrac{140}{3}}\right)}=50,4\left(\dfrac{km}{h}\right)\)
TK
28 tháng 8 2021
Bạn nếu có phát hiện chỗ sai hay ko hiểu về cách giải của mình thì có thể ib hỏi nha. Mình giải có hơi tắt ý. Chúc bạn một ngày tốt lành!
N
17 tháng 11 2021
Đọc lại đề đi bạn, đừng có làm bừa như thế (cop bừa thì đúng hơn chứ nhỉ)
17 tháng 11 2021
Thời gian đi nửa đoạn đường đầu:
\(t_1=\dfrac{S_1}{v_1}=\dfrac{\dfrac{1}{2}S}{v_1}=\dfrac{S}{2v_1}=\dfrac{S}{40}h\)
Thời gian đi nửa đoạn đường sau:
\(t_2=\dfrac{S_2}{v_2}=\dfrac{S}{2v_2}h\)
Vận tốc trung bình:
\(v_{tb}=\dfrac{S}{t_1+t_2}=\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{2v_2}}=48\)
Suy ra v2 nhé.
24 tháng 4 2023
Vận tốc TB của chiếc xe là :
(40 + 60 + 30) : 3 = \(\dfrac{130}{3}\) Km/H
VT
23 tháng 2 2019
Đáp áp D
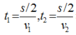
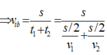
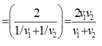
Một vật chuyển động trên n đoạn đường bằng nhau với tốc độ tương ứng là 
thì
17 tháng 8 2021
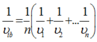
\(400m=0,4km\)
Vận tốc của xe trên nửa quãng đường còn lại là:
\(v_2=\dfrac{v_1}{2}=\dfrac{36}{2}=18\left(km/h\right)\)
Thời gian xe đi trên nửa quãng đường đầu là:
\(t_1=\dfrac{AB}{2v_1}=\dfrac{0,4}{2.36}=\dfrac{1}{180}\left(h\right)\)
Thời gian xe đi trên nửa quãng đường còn lại là:
\(t_2=\dfrac{AB}{2v_2}=\dfrac{0,4}{2.18}=\dfrac{1}{90}\left(h\right)\)
Vận tốc trung bình trên cả quãng đường AB là:
\(v_{tb}=\dfrac{AB}{t_1+t_2}=\dfrac{0,4}{\dfrac{1}{180}+\dfrac{1}{90}}=24\left(km/h\right)\)
H9
HT.Phong (9A5)
CTVHS
18 tháng 6 2023
Gọi s là độ dài nửa quãng đường. Ta có thời gian đi nửa quãng đường đầu là:
\(t_1=\dfrac{s}{v_1}\)
Gọi thời gian ô tô đi nửa phần còn lại là \(t_2\) và \(t_3\) và \(t_2=t_3\)
Thời gian ô tô đi được trong mỗi đoạn này là:
\(s_2=v_2t_2\)
\(s_3=v_3t_3\)
Mà: \(t_2=t_3=\dfrac{s}{v_2+v_3}\)
Vận tốc \(v_3\) là:
\(v_{tb}=\dfrac{2v_1\left(v_2+v_3\right)}{v_2+v_3+2v_1}\) hay \(40=\dfrac{2\cdot30\cdot\left(45+v_3\right)}{45+v_3+2\cdot30}\)
\(\Leftrightarrow40=\dfrac{60\left(45+v_3\right)}{105+v_3}\)
\(\Leftrightarrow40\left(105+v_3\right)=60\left(45+v_3\right)\)
\(\Leftrightarrow2\left(105+v_3\right)=3\left(45+v_3\right)\)
\(\Leftrightarrow210+2v_3=135+3v_3\)
\(\Leftrightarrow3v_3-2v_3=210-135\)
\(\Leftrightarrow v_3=75\left(km/h\right)\)
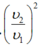
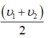
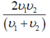
Cách làm:
Tính \(S_1=v_1t_1\)
Sau đó \(S=3S_1\)
\(v_{tb}=\dfrac{S}{t}\Rightarrow\) Tính được \(t\)
Sau đó tính được \(t_2=t-t_1\)
Cuối cùng \(v_2=\dfrac{S_2}{t_2}=\dfrac{S-S_1}{t_2}\)