Giải phương trình x3+2016x2+2016x+2015
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2016x^{2017}+2017y^{2016}=2015\left(1\right)\)
Có 2016x2017 là số chẵn, 2015 là số lẻ
=> 2017y2016 là số lẻ => y2016 là số lẻ
Đặt y1008 = 2k+1 \(\left(k\in Z\right)\)
Có y2016 = (2k+1)2 = 4k2+4k+1
=> 2017y2016 = 2017 (4k2+4k+1) = 2017.4.(k2+k)+2017
Lại có: \(2017.4.\left(k^2+k\right)\equiv0\left(mod4\right)\)
\(2017\equiv1\left(mod4\right)\)
suy ra: \(2017y^{2016}\equiv1\left(mod4\right)\)
mà \(2016x^{2017}\equiv0\left(mod4\right)\)
\(\Rightarrow2016x^{2017}+2017y^{2016}\equiv1\left(mod4\right)\left(2\right)\)
Lại có: \(2015\equiv3\left(mod4\right)\left(3\right)\)
Từ (1), (2) và (3) => PT vô nghiệm


\(\frac{2}{x^2-2015x+2014}=\frac{1}{x^2-2016x+2015}\)
\(\Leftrightarrow\frac{2}{\left(x-1\right)\left(x-2014\right)}=\frac{1}{\left(x-1\right)\left(x-2015\right)}\)
\(\Leftrightarrow\frac{2}{x-2014}=\frac{1}{x-2015}\)
áp dụng tính chất tỉ lệ thức ta có:
\(\frac{2}{x-2014-2}=\frac{1}{x-2015-1}\)
\(\Leftrightarrow\frac{2}{x-2016}-\frac{1}{x-2016}=0\)
\(\Leftrightarrow\left(x-2016\right)\left(2-1\right)=0\)
\(\Leftrightarrow x-2016=0\)
\(\Leftrightarrow x=2016\)

\(2^{2016}.2^{x-1}=2^{2015}\)
\(2^{x-1}=\dfrac{2^{2015}}{2^{2016}}\)
2^2016 . 2^x-1=2^2015
2^x-1=2^2015 : 2^2016
2^x-1= 2^-1
=> x-1= -1
x = -1+1
x = 0

Chọn A.
+Nếu ![]() thì x2 – 1 > 0. Suy ra
thì x2 – 1 > 0. Suy ra 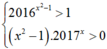
![]() . Do đó phương trình đã cho vô nghiệm.
. Do đó phương trình đã cho vô nghiệm.
+ Nếu -1 < x < 1 thì x2 - 1 < 0. Suy ra 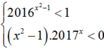
![]() . Do đó phương trình đã cho vô nghiệm.
. Do đó phương trình đã cho vô nghiệm.
+ Kiểm tra x = 1 ; x = -1 thỏa mãn phương trình đã cho.
Vậy phương trình đã cho có hai nghiệm x = -1 ; x = 1.
Suy ra phương trình đã cho có tổng các nghiệm bằng 0.

Chọn C.

=>Phương trình đã cho có 2 nghiệm và tổng hai nghiệm là 0

Chọn D.
Nhẩm pt có 2 nghiệm x = ±1 suy ra loại A
Nếu B đúng thì C đúng suy ra loại B suy ra pt có nhiều hơn 2 nghiệm chọn D.

\(x^3+2016^2+2016x+2015=x^3-1+2016x^2+2016x+2016=\left(x-1\right)\left(x^2+x+1\right)+2016\left(x^2+x+1\right)=\left(x^2+x+1\right)\left(x+2015\right)\)
bạn còn thíêu vế phải nữa