Giải phương trình:\(3x^4-2x^3-52x^2-4x+12=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)

1:
a: =>3x=6
=>x=2
b: =>4x=16
=>x=4
c: =>4x-6=9-x
=>5x=15
=>x=3
d: =>7x-12=x+6
=>6x=18
=>x=3
2:
a: =>2x<=-8
=>x<=-4
b: =>x+5<0
=>x<-5
c: =>2x>8
=>x>4

1
a (9+x)=2 ta có (9+x)= 9+x khi 9+x >_0 hoặc >_ -9
(9+x)= -9-x khi 9+x <0 hoặc x <-9
1)pt 9+x=2 với x >_ -9
<=> x = 2-9
<=> x=-7 thỏa mãn điều kiện (TMDK)
2) pt -9-x=2 với x<-9
<=> -x=2+9
<=> -x=11
x= -11 TMDK
vậy pt có tập nghiệm S={-7;-9}
các cau con lai tu lam riêng nhung cau nhan với số âm thi phan điều kiện đổi chiều nha vd
nhu cau o trên mk lam 9+x>_0 hoặc x>_0
với số âm thi -2x>_0 hoặc x <_ 0 nha

a: \(4x^3+12=120\)
=>\(4x^3=108\)
=>\(x^3=27=3^3\)
=>x=3
b: \(\left(x-4\right)^2=64\)
=>\(\left[{}\begin{matrix}x-4=8\\x-4=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=12\\x=-4\end{matrix}\right.\)
c: (x+1)^3-2=5^2
=>\(\left(x+1\right)^3=25+2=27\)
=>x+1=3
=>x=2
d: 136-(x+5)^2=100
=>(x+5)^2=36
=>\(\left[{}\begin{matrix}x+5=6\\x+5=-6\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x=-11\end{matrix}\right.\)
e: \(4^x=16\)
=>\(4^x=4^2\)
=>x=2
f: \(7^x\cdot3-147=0\)
=>\(3\cdot7^x=147\)
=>\(7^x=49\)
=>x=2
g: \(2^{x+3}-15=17\)
=>\(2^{x+3}=32\)
=>x+3=5
=>x=2
h: \(5^{2x-4}\cdot4=10^2\)
=>\(5^{2x-4}=\dfrac{100}{4}=25\)
=>2x-4=2
=>2x=6
=>x=3
i: (32-4x)(7-x)=0
=>(4x-32)(x-7)=0
=>4(x-8)*(x-7)=0
=>(x-8)(x-7)=0
=>\(\left[{}\begin{matrix}x-8=0\\x-7=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=8\\x=7\end{matrix}\right.\)
k: (8-x)(10-2x)=0
=>(x-8)(x-5)=0
=>\(\left[{}\begin{matrix}x-8=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=5\end{matrix}\right.\)
m: \(3^x+3^{x+1}=108\)
=>\(3^x+3^x\cdot3=108\)
=>\(4\cdot3^x=108\)
=>\(3^x=27\)
=>x=3
n: \(5^{x+2}+5^{x+1}=750\)
=>\(5^x\cdot25+5^x\cdot5=750\)
=>\(5^x\cdot30=750\)
=>\(5^x=25\)
=>x=2

\(a)x^3-\frac{x}{49}=0\)
\(\Leftrightarrow x\left(x^2-\frac{1}{7^2}\right)=0\)
\(\Leftrightarrow x=0\)Hoặc \(x^2-\frac{1}{7^2}=0\)
TH1: \(x\left(x^2-\frac{1}{7^2}\right)=0\\ x=\frac{0}{x^2-\frac{1}{7^2}}\\ \Leftrightarrow x=0\)
TH2: \(x\left(x^2-\frac{1}{7^2}\right)=0\\ x^2-\frac{1}{7^2}=\frac{0}{x}\\ x^2=0+\frac{1}{7^2}\\ x^2=\frac{1}{7^2}\\ x^2=\left(\frac{1}{7}\right)^2\\ \Leftrightarrow x=\frac{1}{7}\)
Vậy \(x=0\)Hoặc \(x=\frac{1}{7}\)
a) x3 - x/49 = 0
<=> x(x2 - 1/49) = 0
<=> x = 0 hoặc x2 - 1/49 = 0
<=> x = 0 hoặc x = +1/7
b) x2 - 7x + 12 = 0
<=> (x - 3)(x - 4) = 0
<=> x - 3 = 0 hoặc x - 4 = 0
<=> x = 3 hoặc x = 4
c) 4x2 - 3x - 1 = 0
<=> 4x2 + x - 4x - 1 = 0
<=> x(4x + 1) - (4x + 1) = 0
<=> (4x + 1)(x - 1) = 0
<=> 4x + 1 = 0 hoặc x - 1 = 0
<=> x = -1/4 hoặc x = 1
d) x3 - 2x - 4 = 0
<=> (x2 + 2x + 2)(x - 2) = 0
vì x2 + 2x + 2 khác 0 nên:
<=> x - 2 = 0
<=> x = 2

Ta có:
\(\sqrt{3x^2+6x+12}+\sqrt{5x^4-10x^2+9}=\sqrt{3\left(x+1\right)^2+9}+\sqrt{5\left(x^2-1\right)^2+4}\ge\sqrt{9}+\sqrt{4}=5\)
\(3-4x-2x^2=5-2\left(x+1\right)^2\le5\)
Đẳng thức xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}3\left(x+1\right)^2=0\\5\left(x^2-1\right)^2=0\\2\left(x+1\right)^2=0\end{matrix}\right.\) \(\Rightarrow x=-1\)
Vậy pt có nghiệm duy nhất \(x=-1\)

a: (3x-2)(4x+5)=0
=>3x-2=0 hoặc 4x+5=0
=>x=2/3 hoặc x=-5/4
b: (2,3x-6,9)(0,1x+2)=0
=>2,3x-6,9=0 hoặc 0,1x+2=0
=>x=3 hoặc x=-20
c: =>(x-3)(2x+5)=0
=>x-3=0 hoặc 2x+5=0
=>x=3 hoặc x=-5/2
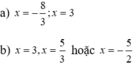
- Với \(x=0\) không phải nghiệm
- Với \(x\ne0\) chia 2 vế cho \(x^2\)
\(\Rightarrow3\left(x^2+\dfrac{4}{x^2}\right)-2\left(x+\dfrac{2}{x}\right)-52=0\)
Đặt \(x+\dfrac{2}{x}=t\Rightarrow t^2=x^2+\dfrac{4}{x^2}+4\Rightarrow x^2+\dfrac{4}{x^2}=t^2-4\)
Pt trở thành:
\(3\left(t^2-4\right)-2t-52=0\)
\(\Leftrightarrow3t^2-2t-64=0\)
Nghiệm của pt này xấu quá
Oh year