Tìm nghiệm nguyên dương của phương trình \(2^x+2^y+2^z=2336 (x< y < z)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
N
0


AH
Akai Haruma
Giáo viên
25 tháng 6 2024
Lời giải:
$4500=2^2.3^2.5^3$
$x< y< z$ nên $x=3$.
Khi đó: $5^3+2.5^y+5^z=4500$
$\Rightarrow 2.5^y+5^z=4375$
$5^y(2+5^{z-y})=4375=5^4.7$
Vì $2+5^{z-y}\not\vdots 5$ với mọi $y< z$ nên $5^y=5^4\Rightarrow y=4$
$\Rightarrow 2+5^{z-y}=7$
$5^{z-4}=5\Rightarrow z-4=1\Rightarrow z=5$
TT
1
BT
0

VT
1

12 tháng 5 2018
2^x +2^y+2^z=2336
2^10<2336<2^11
z>y>x>0
=>z<=10; x>=9
vo nghiem
LH
0

TO
1
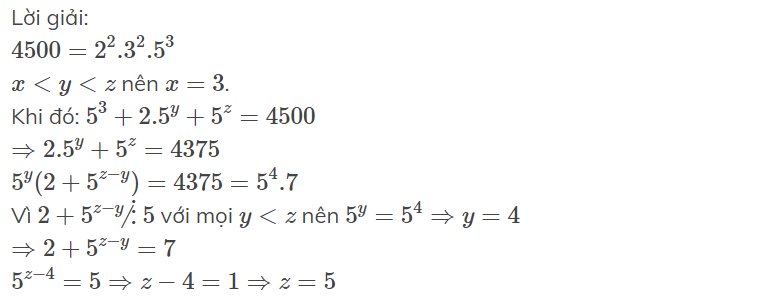
Lời giải:
Do \(x< y< z\) nên từ PT:
\(2^x+2^y+2^z=2336\)
\(\Leftrightarrow 2^x(1+2^{y-x}+2^{z-x})=2336=2^5.73\) (1)
Do \(x< y< z\Rightarrow y-x>0; z-x>0\)
Do đó \(1+2^{y-x}+2^{z-x}\) lẻ (2)
Từ (1)(2) suy ra \(\left\{\begin{matrix} 2^x=2^5\\ 1+2^{y-x}+2^{z-x}=73\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x=5\\ 2^{y-x}+2^{z-x}=72\end{matrix}\right.\)
\(\Rightarrow 2^{y-5}+2^{z-5}=72\)
\(\Leftrightarrow 2^{y-5}(1+2^{z-y})=72=2^3.3^2\)
Vì \(y< z\Rightarrow z-y>0\Rightarrow 1+2^{z-y}\) lẻ. Mặt khác $2^{y-5}$ chỉ chứa ước nguyên tố là $2$
Do đó: \(\left\{\begin{matrix} 2^{y-5}=2^3\\ 1+2^{z-y}=3^2\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} y=8\\ 2^{z-y}=8\end{matrix}\right.\Rightarrow y=8; z=11\)
Vậy \((x,y,z)=(5,8,11)\)