Hãy chon mệnh đề sai dưới đây:(mn chọn rồi giải thích từng đáp án giúp e với ạ, có thể bỏ qua đáp án A , còn đáp án B tại sao x phải >0 ạ , đáp án C e ko chắc lắm nên mn cứ gthich đi ạ, còn đáp án D có phải thêm đk của c không hay như vậy vẫn đúng ạ )
A. \(\int\limits^1_0x^2dx\ge\int\limits^1_0x^3dx\)
B. đạo hàm của F(x)= \(\int\limits^x_1\dfrac{dt}{1+t}\) là F'(x)= \(\dfrac{1}{1+x}\) (x>0)
C.hàm số f(x) liên tục trên \([-a;a]\) thì \(\int\limits^a_{-a}f\left(x\right)dx=2\int\limits_0^af\left(x\right)dx\)
D.nếu f(x) liên tục trên R thì \(\int\limits^b_af\left(x\right)dx+\int\limits^c_bf\left(x\right)dx=\int\limits^c_af\left(x\right)dx\)





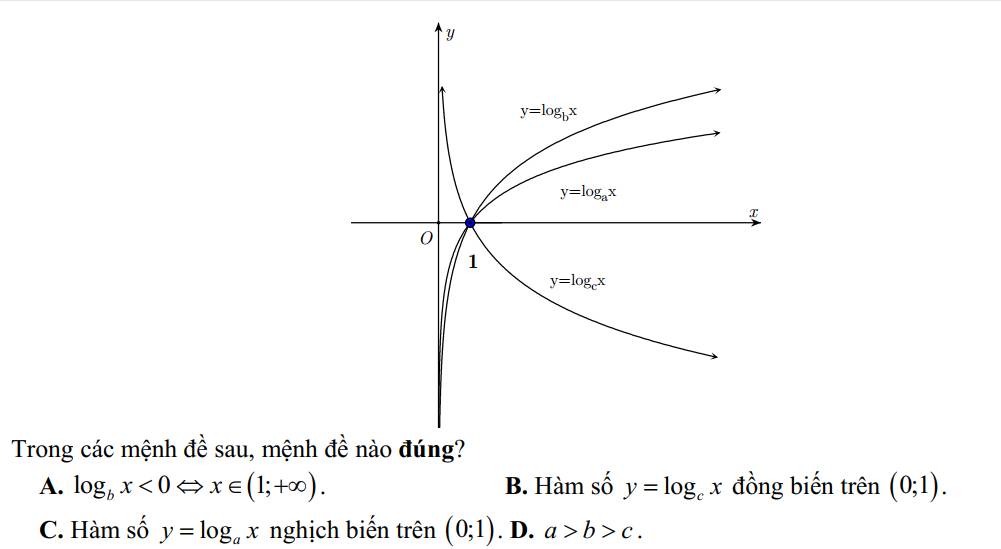
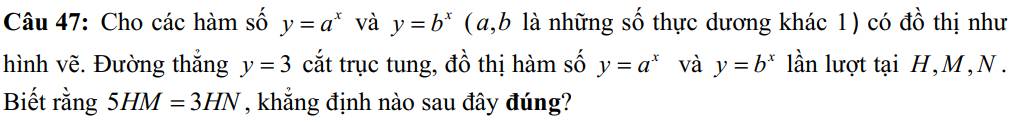
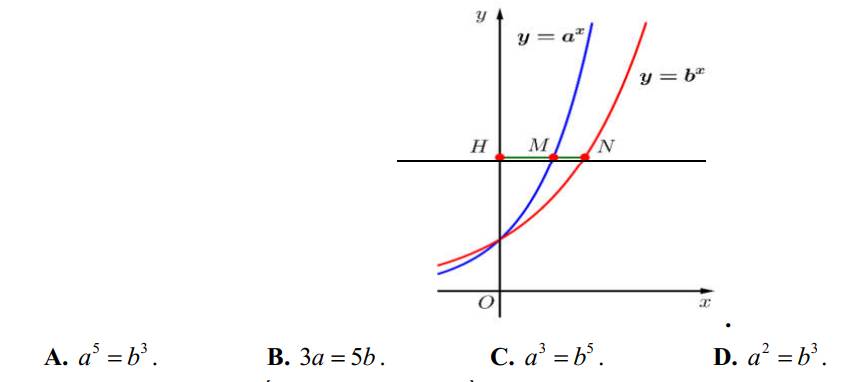
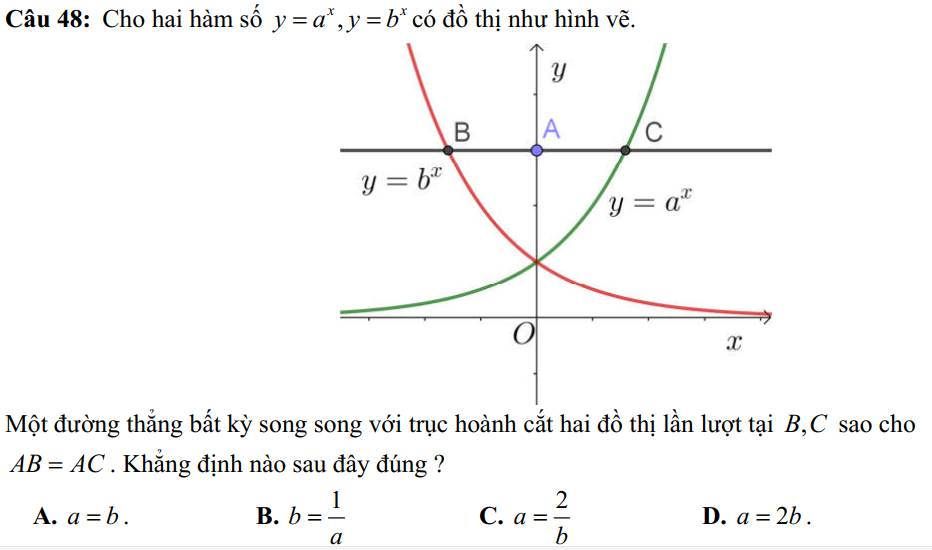



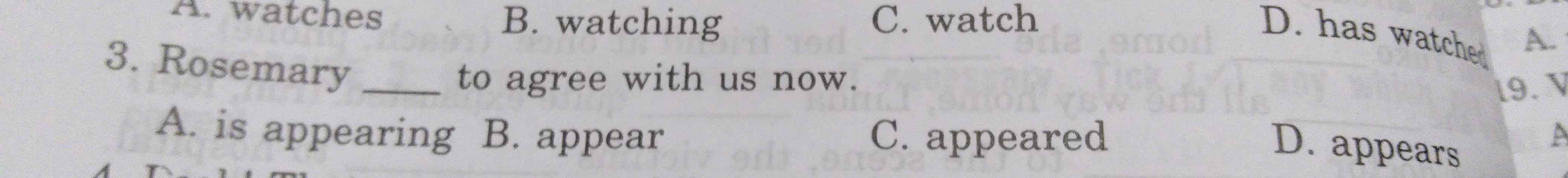



 giúp mình làm phần test 4 với ạ, chỉ cần ghi đáp án thôi ạ. Đáp án cũ chưa chắc đúng nên cần gợi ý ạ
giúp mình làm phần test 4 với ạ, chỉ cần ghi đáp án thôi ạ. Đáp án cũ chưa chắc đúng nên cần gợi ý ạ
Lời giải:
\(\int ^{1}_{0}x^2dx=\left.\begin{matrix} 1\\ 0\end{matrix}\right|\frac{x^3}{3}=\frac{1}{3}; \int ^{1}_{0}x^3dx=\left.\begin{matrix} 1\\ 0\end{matrix}\right|\frac{x^4}{4}=\frac{1}{4}\)
\(\frac{1}{3}>\frac{1}{4}\Rightarrow A\) đúng.
Câu B. Xét về mặt điều kiện thì với \(x>0\Rightarrow \frac{1}{x+1}\) luôn có nghĩa, lúc này hàm số mới có tích phân được.
Xét theo định nghĩa nguyên hàm thì luôn đúng vì \(F(x)=\int f(x)dx\Leftrightarrow f(x)=F'(x)\)
Câu D.
\(\int ^b_af(x)dx+\int ^c_bf(x)dx=F(b)-F(a)+F(c)-F(b)\)
\(=F(c)-F(a)=\int ^c_af(x)dx\)
Do đó D đúng.
Do đó câu C sai.
Nếu \(\int ^a_{-a}f(x)dx=2\int ^{a}_0f(x)dx\)
\(\Leftrightarrow F(a)-F(-a)=2F(a)-2F(0)\)
\(\Leftrightarrow F(a)+F(-a)=2F(0)\)
Giả sử cho \(F(x)=x^2\), \(a\neq 0\)thì điều trên hiển nhiên vô lý
Do đó C sai.