a,trên cùng một hệ trục tọa độ vẽ các ĐTHS sau : (d1): y=-2x+5 ; (d2) : y = x+ 2
b, xác định tọa độ gđ của A của (d1) và (d2)
c, xác định hs có có đồ thị đi qua gốc tọa O và điểm A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Vẽ đồ thị của hàm số y = x
Cho x = 0 thì y = 0
Cho x = 1 thì y = 1
Đồ thị hàm số y = x là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm (1; 1)
*Vẽ đồ thị hàm số y = 2x
Cho x = 0 thì y = 0
Cho x = 1 thì y = 2
Đồ thị hàm số y = 2x là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm (1;2)
*Vẽ đồ thị của hàm số y = -x + 3
Cho x = 0 thì y = 3. Ta có điểm (0; 3)
Cho y = 0 thì x = 3. Ta có điểm (3; 0)
Đồ thị hàm số y = -x + 3 là đường thẳng đi qua hai điểm (0; 3) và (3; 0)

b: Phương trình hoành độ giao điểm là:
\(2x+2=\dfrac{-1}{2}x-2\)
\(\Leftrightarrow x\cdot\dfrac{5}{2}=-4\)
hay x=-10
Thay x=-10 vào (d1), ta được:
\(y=-20+2=-18\)

a, bạn tự vẽ nhé
b, Hoành độ giao điểm thỏa mãn phương trình
\(2x-3=-3x+7\Leftrightarrow5x=10\Leftrightarrow x=2\)
Thay vào ptđt d1 ta được : \(y=4-3=1\)
Vậy d1 cắt d2 tại A(2;1)

a: 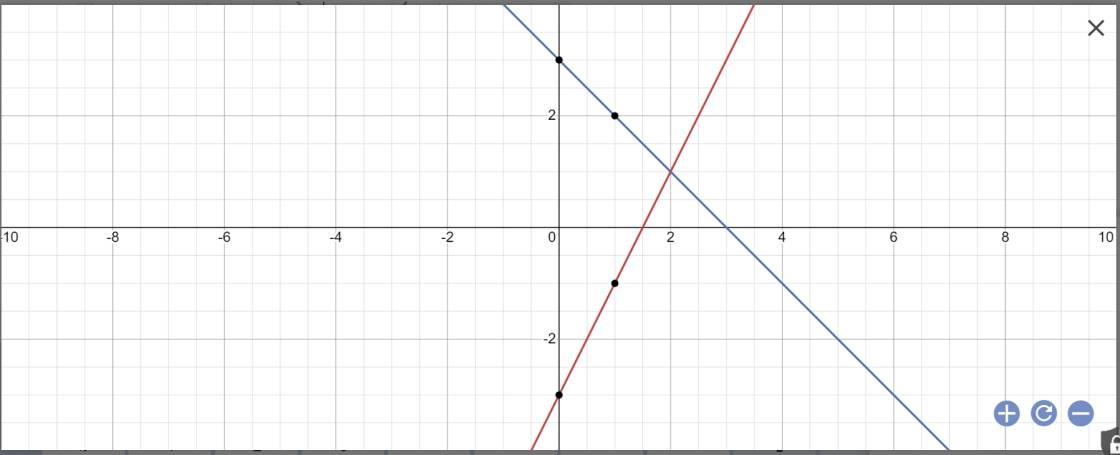
b: Phương trình hoành độ giao điểm là:
2x-3=3-x
=>3x=6
=>x=6/3=2
Thay x=2 vào y=3-x, ta được:
\(y=3-2=1\)
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-2x+5=x+2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
c: Gọi (D): y=ax+b là phương trình đường thẳng cần tìm
Vì (D) đi qua A(1;3) và O(0;0) nên tacó hệ phương trình:
\(\left\{{}\begin{matrix}a+b=3\\a\cdot0+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=0\end{matrix}\right.\)
Vậy: y=3x