Tia phân giác là j zợ😅
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hải Môn (chữ Hán phồn thể: 海門市, chữ Hán giản thể: 海门市) là một thị xã thuộc địa cấp thị Nam Thông, tỉnh Giang Tô, Cộng hòa Nhân dân Trung Hoa. Thị xã này được lập tháng 6 năm 1994 trên cơ sở huyện. Hải Môn có diện tích 1001 ki-lô-mét vuông, dân số 1,01 triệu người. Mã số bưu chính là 226100. Chính quyền thị xã đóng ở trấn Hải Môn. Về mặt hành chính, thị xã này được chia thành 20 trấn, 1 hương và 2 khu phát triển kinh tế cấp huyện.

Xét ΔDBC có
BA là đường trung tuyến
BA=DC/2
Do đó: ΔDCB vuông tại B

Vì oy là tia phân giác xoz
=> xoy = yoz
mà xoy = 45 độ
=> yoz = 45 độ
ta có : xoy + yoz = xoz
=> 45 + 45 = xoz
=> xoz = 90 độ
=> xoz là góc vuông.
Học tốt!!!


- Nội dung : Nghiên cứu cơ sở vật chất, cơ chế di truyền, tính quy luật của hiện tượng biến dị và di truyền để giải thích tại sao con cái sinh ra giống bố mẹ, tổ tiên trên những nét lớn nhưng lại khác bố mẹ tổ tiên trên hàng loạt các đặc điểm khác.
- Ý nghĩa : Di truyền học đã trở thành ngành mũi nhọn trong sinh học hiện đại. Biến dị và di truyền là cơ sở lí thuyết của khoa học chọn giống, sử dụng để phát hiện nguyên nhân, cơ chế của bệnh, tật di truyền để đề xuất các lời khuyên phù hợp trong tư vấn di truyền học và đặc biệt có tầm quan trọng trong công nghiệp sinh học hiện đại.
-Nội dung:
+Các quy luật và định luật di truyền : quy luật phân li , định luật phân li độc lập , di truyền liên kết ,hoán vị gen ...v...v
+Quy luật của các loại biến dị (đột biến NST , đột biến gen...)và nguyên nhân gây ra các
đột biến (tác nhân hóa học ,vật lí.....v...v)
+cơ sở vật chất và cơ chế của hiện tượng di truyền
- Ý nghĩa thực tiễn: đóng vai trò quan trọng cho Khoa học chọn giống, Y học đặc biệt là trong công nghệ sinh học hiện đại(ví dụ : .ngày nay ta có thể tạo ra giống đậu có hàm lượng vitamin A cao chống bệnh khô mắt ,những giống lúa cho năng suất cao đặc biệt ta có thể biết tỉ lệ khuyết tật của thai nhi cũng như khả năng của đúa trẻ trong tương lai)

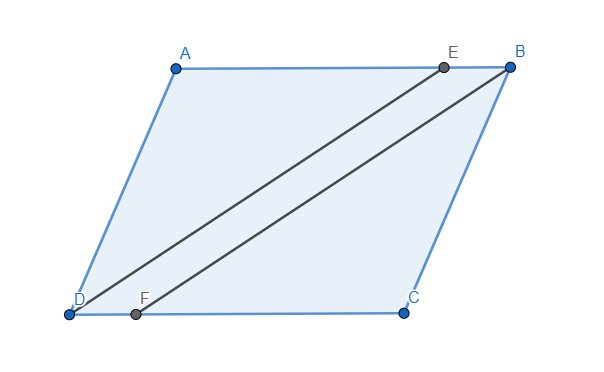
a) Ta thấy \(\widehat{AED}=\widehat{EDC}=\widehat{ADE}\) nên tam giác ADE cân tại A. Hoàn toàn tương tự thì tam giác CBF cân tại C.
Mặt khác, do tứ giác ABCD là hình bình hành nên \(\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}\). Do đó \(\dfrac{\widehat{B}}{2}=\dfrac{\widehat{D}}{2}\) hay \(\widehat{CBF}=\widehat{ADE}\). Kết hợp với \(\widehat{A}=\widehat{C}\) thì suy ra \(\Delta ADE~\Delta CBF\left(g.g\right)\). Lại có \(\dfrac{AD}{CB}=1\) (do tứ giác ABCD là hình bình hành), suy ra \(\Delta ADE=\Delta CBF\) (2 tam giác đồng dạng có tỉ số đồng dạng bằng 1 thì 2 tam giác đó bằng nhau), ta có đpcm.
b) Ta thấy \(\widehat{AED}=\widehat{ADE}=\widehat{CBF}=\widehat{ABF}\) nên DE//BF. Lại có BE//DF (do tứ giác ABCD là hình bình hành) nên tứ giác DEBF cũng là hình bình hành (các cặp cạnh đối song song).
A B C D E F
a/
Xét tg ADE có
\(\widehat{ADE}=\widehat{CDE}\) (gt) (1)
\(\widehat{AED}=\widehat{CDE}\) (góc so le trong) (1)
Từ (1) và (2) => \(\widehat{ADE}=\widehat{AED}\) => tg ADE là tg cân tại A
=> AD=AE (3)
Xét tg CBF có
\(\widehat{CBF}=\widehat{ABF}\) (gt) (4)
\(\widehat{CFB}=\widehat{ABF}\) (góc so le trong) (5)
Từ (4) và (5) => \(\widehat{CBF}=\widehat{CFB}\) => tg CBF cân tại C
=> CB=CF (6)
Ta có
AD=CB (cạnh đối hình bình hành) (7)
Từ (3) (6) (7) => AD=AE=CB=CF
Mà \(\widehat{DAE}=\widehat{BCF}\) (góc đối hình bình hành)
=> tg ADE = tg CBF (c.g.c)
=> tg ADE và tg CBF là những tg cân bằng nhau
b/
tg ADE = tg CBF (cmt) \(\Rightarrow\widehat{BFC}=\widehat{ADE}\)
Mà \(\widehat{EDC}=\widehat{ADE}\) (gt)
\(\Rightarrow\widehat{BFC}=\widehat{EDC}\) Hai góc này ở vị trí đồng vị => DE//BF (8)
Ta có
AB//CD (cạnh đối hình bình hành) => BE//DF (9)
Từ (8) (9) => DEBF là hình bình hành (tứ giác có các cặp cạnh đối // với nhau là hình bình hành)
tia phân giác là tia nằm giữa 2 cạnh của góc và tạo vs 2 cạnh ấy bằng 2 góc bằng nhau
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.