Tổng S = 31+32+33+......+32012 có chia hết cho 120 . Vì sao
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tổng trên = (31+32012).[(32012-31:1+1] : 2 = 32043 . 31982 : 2 = 42043 . 15991 lẻ
=> tổng trên ko chia hết cho 120
k mk nha

không chia hết cho 120 vì tổng trên là số lẻ nên không chia hết cho một số chẵn

Tổng 31 + 32 + 33 + 34 + 35 + … + 32012 không chia hết cho 120 vì tổng trên là một số lẻ, không chia hết cho một số chẵn.
tổng trên không chia hết cho 120. Vì các số trên có tổng là số lẻ lên không chia hết cho số chẵn

\(A=3+3^2+3^3+...+3^{2012}\\ A=\left(3+3^2+3^3+3^4\right)+...+\left(3^{2009}+3^{2010}+3^{2011}+3^{2012}\right)\\ A=120+...+3^{2008}.120\\ A=120.\left(1+...+3^{2008}\right)⋮120\)

\(B=3+3^2+3^3+3^4+...+3^{2009}+3^{2010}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2009}\left(1+3\right)\)
\(=4.\left(3+3^3+...+3^{2009}\right)\)
⇒ \(B\) ⋮ 4
b: \(C=5\left(1+5+5^2\right)+...+5^{2008}\left(1+5+5^2\right)=31\cdot\left(5+...+5^{2008}\right)⋮31\)

\(B=3+3^2+3^3+...+3^{60}\)
\(=3\left(1+3+3^2\right)+...+3^{58}\left(1+3+3^2\right)\)
\(=13\left(3+...+3^{58}\right)⋮13\)

Số số hạng của B:
60 - 1 + 1 = 60 (số)
Do 60 ⋮ 3 nên ta có thể nhóm các số hạng của B thành từng nhóm mà mỗi nhóm có 3 số hạng như sau:
B = (3 + 3² + 3³) + (3⁴ + 3⁵ + 3⁶) + ... + (3⁵⁸ + 3⁵⁹ + 3⁶⁰)
= 3.(1 + 3 + 3²) + 3⁴.(1 + 3 + 3²) + ... + 3⁵⁸.(1 + 3 + 3²)
= 3.13 + 3⁴.13 + ... + 3⁵⁸.13
= 13.(3 + 3⁴ + ... + 3⁵⁸) ⋮ 13
Vậy B ⋮ 13

\(A=3+3^2+3^3+...+3^{2020}=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2019}.\left(1+3\right)=\left(1+3\right)\left(3+3^3+...+3^{2019}\right)=4.\left(3+3^3+...+3^{2019}\right)⋮4\)
A=3 + 32 + 33 + ... + 32020 =3 (1 + 3) + 33 (1 + 3) + ... + 32019 . (1 + 3)
=(1 + 3)(3 + 33+...+32019)=4 . ( 3 + 33+ ... + 32019) ⋮ 4
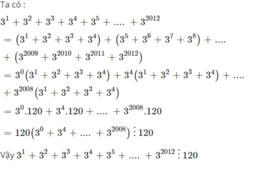
Ta có : \(3^1=3;3^2=9;3^3=27;3^4=81\)
Do đó : \(3^1+3^2+3^3+3^4=3+9+27+81=120\)
Nên \(3^1+3^2+3^3+3^4+3^5+...+3^{2012}=\left(3^1+3^2+3^3+3^4\right)+\left(3^5+3^6+3^7+3^8\right)+...+\left(3^{2009}+3^{2010}+3^{2011}+3^{2012}\right)=120+3^4.120+...+3^{2008}.120=120.\left(1+3^4+...+3^{2008}\right)⋮120\) Vậy tổng \(S=3^1+3^2+3^3+...+3^{2012}⋮120\)