 Tính S tô đậm, gửi lại ạ! Mong mn giúp hứa sẽ tick!
Tính S tô đậm, gửi lại ạ! Mong mn giúp hứa sẽ tick!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Nhân cả 2 vế với \(\left(x+\sqrt{x^2+5}\right)\left(y+\sqrt{y^2+5}\right)\)ta được 25=5\(\left(x+\sqrt{x^2+5}\right)\left(y+\sqrt{y^2+5}\right)\)
<=> \(\left(x+\sqrt{x^2+5}\right)\left(y+\sqrt{y^2+5}\right)\)= 5 = \(\left(x-\sqrt{x^2+5}\right)\left(y-\sqrt{y^2+5}\right)\)
khai triển và rút gọn ta được \(x\sqrt{y^2+5}=-y\sqrt{x^2+5}\)
Nếu x=y=0 => M=0
xét x;y khác 0
\(\frac{\sqrt{x^2+5}}{\sqrt{y^2+5}}=\frac{-x}{y}\left(\frac{x}{y}< 0\right)\)<=>\(\frac{x^2+5}{y^2+5}=\frac{x^2}{y^2}=\frac{x^2+5-x^2}{y^2+5-y^2}=1=>\frac{x^2}{y^2}=1=>\frac{x}{y}=-1\left(\frac{x}{y}< 0\right).\)
hay x=-y => M= (-y)2017 +y2017 =0
vậy M=0


\(S_{ABM}=\dfrac{1}{2}AH.BM\)
\(\Rightarrow27,9=\dfrac{1}{2}.AH.9\)
\(\Rightarrow AH=6,2\left(cm\right)\)
Diện tích phần tô đậm là:
\(S_{AMC}=\dfrac{1}{2}AH.MC=\dfrac{1}{2}.6,2.4=12,4\left(cm^2\right)\)

a: ΔABC vuông tại B
=>\(\widehat{A}+\widehat{C}=90^0\)
=>\(\widehat{A}=50^0\)
Xét ΔBAC vuông tại B có
\(sinC=\dfrac{AB}{AC}\)
=>\(AC=\dfrac{6}{sin40}\simeq9,33\left(cm\right)\)
ΔBAC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BC=\sqrt{9.33^2-6^2}\simeq7,14\left(cm\right)\)
b: ΔBAC vuông tại B có BH là đường cao
nên \(HC\cdot HA=BH^2\left(1\right)\)
ΔBHC vuông tại H có HI là đường cao
nên \(BI\cdot BC=BH^2\left(2\right)\)
Từ (1),(2) suy ra \(HC\cdot HA=BI\cdot BC\)
c: ΔBHA vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\left(3\right)\)
Từ (2),(3) suy ra \(BI\cdot BC=BM\cdot BA\)
=>\(\dfrac{BI}{BA}=\dfrac{BM}{BC}\)
Xét ΔBIM vuông tại B và ΔBAC vuông tại B có
\(\dfrac{BI}{BA}=\dfrac{BM}{BC}\)
Do đó: ΔBIM đồng dạng với ΔBAC



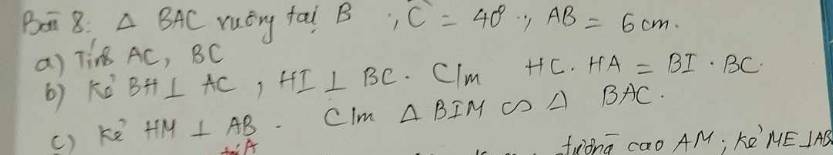

S=A x A