B1)Tìm x,y biết:
\(\dfrac{2x}{3}=\dfrac{5y}{4}\) và x + y = \(\dfrac{1}{2}\)
B2) Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\). Chứng minh rằng ta có các tỉ lệ thức sau ( giả thiết các tỉ lệ thức đều có nghĩa ):
1/ \(\dfrac{a+b}{b}=\dfrac{c+d}{d}\) 2/ \(\dfrac{2a+3b}{2a-3b}=\dfrac{2c+3d}{2c-3d}\)
B3) Cho x và y là 2 đại lg tỉ lệ thuận, x1 và x2 là 2 giá trị khác nhau của x, y1 và y2 là 2 giá trị tương ứng của y. Tính x1, biết y1 = -3; y2 = -2; x2 = 5.
B4) Tìm giá trị lớn nhất và nhỏ nhất(nếu có) các biểu thức sau:
a) P = 3,7 + |4,3 - x| b) Q = 5,5 - |2x - 1,5|
B5) Cho △ABC. Trên tia đối của tia CB lấy điểm M sao cho CM = CB. Trên tia đối của tia CA lấy điểm D sao cho CD = CA.
a) CMinh △ABC = △DMC
b) CMinh MD // AB
c) Gọi I là 1 điểm nằm giữa A và B. Tia IC cắt MD tại điểm N. So sánh độ dài các đoạn thẳng BI và NM, IA và ND
~~ Giúp mik nha mn, mik gấp liếm !!!!( B5 các bạn k cần vt GT, KL đâu nha)

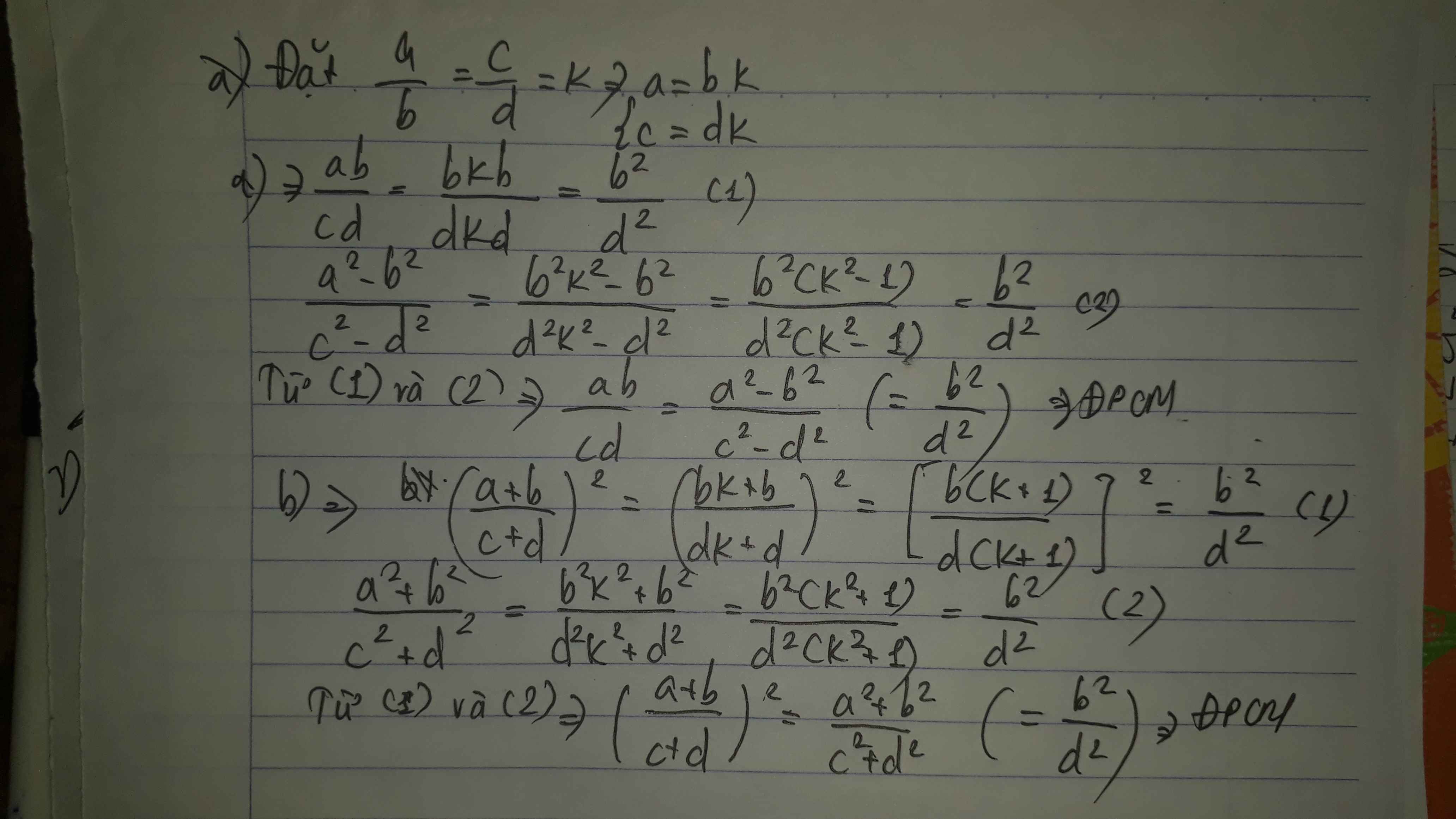
Bài 1:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{5}}=\dfrac{x+y}{\dfrac{3}{2}+\dfrac{4}{5}}=\dfrac{0.5}{2.3}=\dfrac{5}{23}\)
Do đó: x=15/46; y=4/23
Bài 2:
1: Đặt a/b=c/d=k
=>a=bk; c=dk
\(\dfrac{a+b}{b}=\dfrac{bk+b}{b}=k+1\)
\(\dfrac{c+d}{d}=\dfrac{dk+d}{d}=k+1\)
Do đó: \(\dfrac{a+b}{b}=\dfrac{c+d}{d}\)