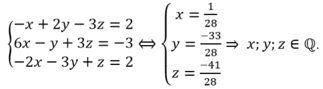Tìm nghiệm nguyên của hệ phương trình sau (x +y+ z)/2=50 và (5x+ 3y +z)/3=100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
0
NN
Tìm nghiệm nguyên dương của hệ phương trình sau
\({x +y+z \over 2}=50 \) và \(5x+3y+{z \over 3}=100\)
0
CC
0
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 1 2021
\(\left\{{}\begin{matrix}15x+9y+z=300\\x+y+z=100\end{matrix}\right.\)
\(\Rightarrow14x+8y=200\Rightarrow7x+4y=100\)
\(\Leftrightarrow7x=4\left(25-y\right)\)
Do 7 và 4 nguyên tố cùng nhau \(\Rightarrow x⋮4\Rightarrow x=4k\)
\(\Rightarrow y=25-7k\)
\(z=100-\left(x+y\right)=3k+75\)
Vậy nghiệm của pt là \(\left(x;y;z\right)=\left(4k;-7k+25;3k+75\right)\) với \(k\in Z\)
16 tháng 10 2019
\(\hept{\begin{cases}x+y+z=100\\5x+3y+\frac{z}{5}=60\end{cases}}\)
<=> \(\hept{\begin{cases}x+y+z=100\\25x+15y+z=300\end{cases}}\)
Trừu vế dưới vơi vế trên:
\(24x+14y=200\)
<=> \(12x+7y=100\)
Có : \(12x⋮4,100⋮4\Rightarrow7y⋮4\Rightarrow y⋮4\)
Đặt: y = 4k, k nguyên dương
Có: \(12x+28k=100\)
<=> \(3x+7k=25\)Vì x, k nguyên dương
Chọn k = 1 => x = 6 TM. Vậy y = 4, x =6, z =90
Chọn k = 2 => x =11/3 loại
Chọn k= 3 => x =4/3 loại
Chọn \(k\ge4\)=> \(25=3x+28>28\) vô lí.
Vậy x = 6; y= 4, z = 90.
16 tháng 10 2019
Câu hỏi của Trâm Anh - Toán lớp 9 - Học toán với OnlineMath
