x2-3xy2-3x2y - y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PM
3
28 tháng 10 2021
c) \(3x+3y-x^2-2xy-y^2=3\left(x+y\right)-\left(x+y\right)^2=\left(x+y\right)\left(3-x-y\right)\)d) \(=\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\)
\(=\left(x+y\right)\left(x+y+1\right)\left(x+y-1\right)\)
28 tháng 10 2021
\(c,=3\left(x+y\right)-\left(x+y\right)^2=\left(3-x-y\right)\left(x+y\right)\\ d,=\left(x+y\right)^3-\left(x+y\right)=\left(x+y\right)\left[\left(x+y\right)^2-1\right]\\ =\left(x+y\right)\left(x+y-1\right)\left(x+y+1\right)\)
MN
Phân tích đa thức này thành nhân...
Đọc tiếp
Phân tích đa thức này thành nhân tử.
x3−3x2y+3xy2−y3+y2−x2
2
NH
2
11 tháng 8 2021
a) Ta có: \(M=x^2-2xy+y^2-10x+10y\)
\(=\left(x-y\right)^2-10\left(x-y\right)\)
\(=9^2-10\cdot9=-9\)
CM
13 tháng 1 2018
Ta có
N = x 3 + 3 x 2 y + 3 x y 2 + y 3 + x 2 + 2 x y + y 2 = ( x 3 + 3 x 2 y + 3 x y 2 + y 3 ) + ( x 2 + 2 x y + y 2 ) = ( x + y ) 3 + ( x + y ) 2 = ( x + y ) 2 ( x + y + 1 )
Từ đề bài x = 10 – y ó x + y = 10. Thay x + y = 10 vào N = ( x + y ) 2 (x + y + 1) ta được
N = 10 2 (10 + 1) = 1100
Suy ra N > 1000 khi x = 10 – y
Đáp án cần chọn là: D
21 tháng 7 2023
`a, x^3 + y^3 + x + y`
`= (x+y)(x^2-xy+y^2)+x+y`
`= (x+y)(x^2-xy+y^2+1)`
`b, x^3 - y^3 + x -y`
`= (x-y)(x^2+xy+y^2)+x-y`
`= (x-y)(x^2+xy+y^2+1)`
`c, (x-y)^3 + (x+y)^3`
`= (x-y+x+y)(x^2-2xy+y^2 - x^2 + y^2 + x^2 + 2xy + y^2)`
`= (2x)(x^2 + 3y^2)`
`d, x^3 - 3x^2y + 3xy^2 - y^3 + y^2 - x^2`
`= (x-y)^3 + (y-x)(x+y)`
`=(x-y)(x^2+2xy+y^2-x-y)`
21 tháng 7 2023
a: =(x+y)(x^2-xy+y^2)+(x+y)
=(x+y)(x^2-xy+y^2+1)
b: =(x-y)(x^2+xy+y^2)+(x-y)
=(x-y)(x^2+xy+y^2+1)
c: =x^3-3x^2y+3xy^2-y^3+x^3+3x^2y+3xy^2-y^3
=2x^3+6xy^2
d: =(x-y)^3+(y-x)(y+x)
=(x-y)[(x-y)^2-(x+y)]
H9
HT.Phong (9A5)
CTVHS
12 tháng 8 2023
a) \(\left(\dfrac{3}{5}a^6x^3+\dfrac{3}{7}a^3x^4-\dfrac{9}{10}ax^5\right):\dfrac{3}{5}ax^3\)
\(=\dfrac{\dfrac{3}{5}a^6x^3+\dfrac{3}{7}a^3x^4-\dfrac{9}{10}ax^5}{\dfrac{3}{5}ax^3}\)
\(=\dfrac{\dfrac{3}{5}ax^3\left(a^5+\dfrac{5}{7}a^2x-\dfrac{3}{2}x^2\right)}{\dfrac{3}{5}ax^3}\)
\(=a^5+\dfrac{5}{7}a^2x-\dfrac{3}{2}x^2\)
b) \(\left(9x^2y^3-15x^4y^4\right):3x^2y-\left(2-3x^2y\right)\cdot y^2\)
\(=\dfrac{3x^2y\left(3y^2-5x^2y^3\right)}{3x^2y}-2y^2+3x^2y^3\)
\(=3y^2-5x^2y^3-2y^2+3x^2y^3\)
\(=y^2-2x^2y^3\)
H9
HT.Phong (9A5)
CTVHS
12 tháng 8 2023
c) \(\left(6x^2-xy\right):x+\left(2x^3y+3xy^2\right):xy-\left(2x-1\right)x\)
\(=\dfrac{6x^2-xy}{x}+\dfrac{2x^3y+3xy^2}{xy}-x\left(2x-1\right)\)
\(=\dfrac{x\left(6x-y\right)}{x}+\dfrac{xy\left(2x^2+3y\right)}{xy}-2x^2+x\)
\(=6x-y+2x^2+3y-2x^2+x\)
\(=7x+2y\)
d) \(\left(x^2-xy\right):x+\left(6x^2y^5-9x^3y^4+15x^4y^2\right):\dfrac{3}{2}x^2y^3\)
\(=\dfrac{x^2-xy}{x}+\dfrac{6x^2y^5-9x^3y^4+15x^4y^2}{\dfrac{3}{2}x^2y^3}\)
\(=\dfrac{x\left(x-y\right)}{x}+\dfrac{\dfrac{3}{2}x^2y^2\left(4y^3-6xy^2+10x^2\right)}{\dfrac{3}{2}x^2y^3}\)
\(=x-y+\dfrac{4y^3-6xy^2+10x^2}{y}\)
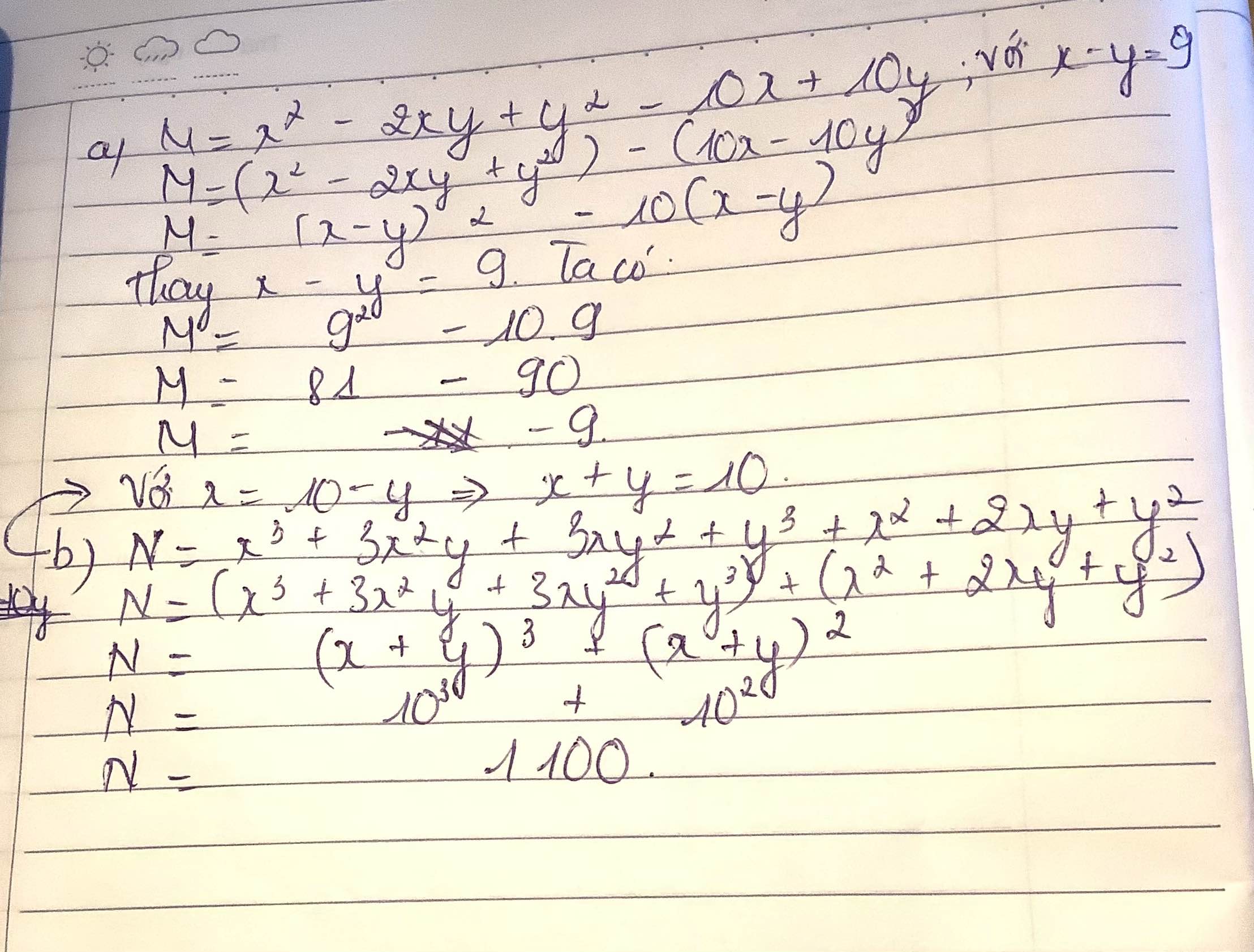
\(x^2-3xy^2-3x^2y-y^2\)
\(=\left(x^2-y^2\right)-\left(3xy^2+3x^2y\right)\)
\(=\left(x-y\right)\left(x+y\right)-3xy\left(y+x\right)\)
\(=\left(x-y\right)\left(x+y\right)-3xy\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-3xy\right)\)
x2-3xy2-3x2y - y2
=(x2-y2)-(3xy2+3x2y)
=(x-y)(x+y)-3xy(y+x)
=(x+y)(x-y-3xy)