x25y chia hết cho cả 2,5 và chia cho 3 dư 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 7 2015
a) 5x2y chia hết cho cả 2 và 5 => y= 0
Số đó chia hết cho 9 nên 5 + x + 2 = 7+ x chia hết cho 9 => x = 2
Vậy số đó là: 5220
b) số đó chia hết cho 5 nên y = 0 hoặc y = 5
Với y = 0 : Số đó chia hết cho 3 thì 7 + x chia hết cho 3 => x = 2 hoặc x = 5; x = 8. Các số tương ứng là: 5220; 5520; 5820
Với y = 5 : số đó chia hết cho 5 thì tổng 12 + x chia hết cho 3 => x = 0 ; x = 3; x = 6; x = 9 Các số tương ứng là: 5025; 5325; 5625; 5925
c) chia cho 2 dư 1 => y lẻ => y = 1;3;5;7;9
mà số đó chia cho 5 dư 4 => y = 4 hoặc 9. Kết hợp với điều kiện trên => y = 9
Số đó chia hết cho 9 nên 7 +x + y chia hết cho 9
Vì y = 9 => 7 + x + 9 = 16 + x chia hết cho 9 => x = 2
Vậy số cần tìm là: 5229
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
8 tháng 11 2021
a/
\(\overline{4x6y}⋮2;\overline{4x6y}⋮5\Rightarrow y=0\Rightarrow\overline{4x6y}=\overline{4x60}\)
\(\Rightarrow\overline{4x60}-1=\overline{4x59}⋮3\Rightarrow4+x+5+9=18+x⋮9\Rightarrow x=\left\{0;9\right\}\)
b/
\(\overline{57x2y}\) không chia hết cho 2 => y lẻ
\(\overline{57x2y}⋮5\Rightarrow y=5\)
\(\Rightarrow\overline{57x2y}=\overline{57x25}⋮9\Rightarrow5+7+x+2+5=19+x⋮9\Rightarrow x=8\)
CX
30 tháng 1 2020
=) 1a23b \(⋮\)2;5 =) b = 0 hay ta có số : 1a230
=) 1a230 : 9 dư 4 =) ( 1a230 - 4 ) \(⋮\)9 =) 1a226 \(⋮\)9
=) 1+a+2+2+6 \(⋮\) 9
=) 11+a \(⋮\)9
=) a = 7
vậy số đó là : 17230
30 tháng 1 2020
Ta có:1a23b chia cho 9 dư 4 thì tổng các chữ số bắt buộc phải là 13.
\(\Rightarrow\)Số đó có thể là:17230;13234;14233;12235;15232;11236;15231
Nhưng đầu bài cho là số đó chia hết cho 5 vậy tận cùng số đó sẽ là 5 hoặc 0
\(\Rightarrow\)Các số đó là:17230;12235
Ta thử:17230:2,5=6892( chọn )
12235:2,5=4894( chọn )
Cả 2 số này đều thỏa mãn đề bài nên số có dạng 1a23b mà chia hết cho 2,5 nhưng khi chia cho 9 dư 4 là:17230;12235
30 tháng 12 2018
A= 4p+3 = 17m+9= 19n+13
A+25 =4p+28= 17m+34 =19n+38
nhận thấy A+25 đồng thời chia hết cho 4, 17 và 19
vậy A+25 chia hết cho 4.17.19 =1292
A chia 1292 dư (1292-25) = 1267
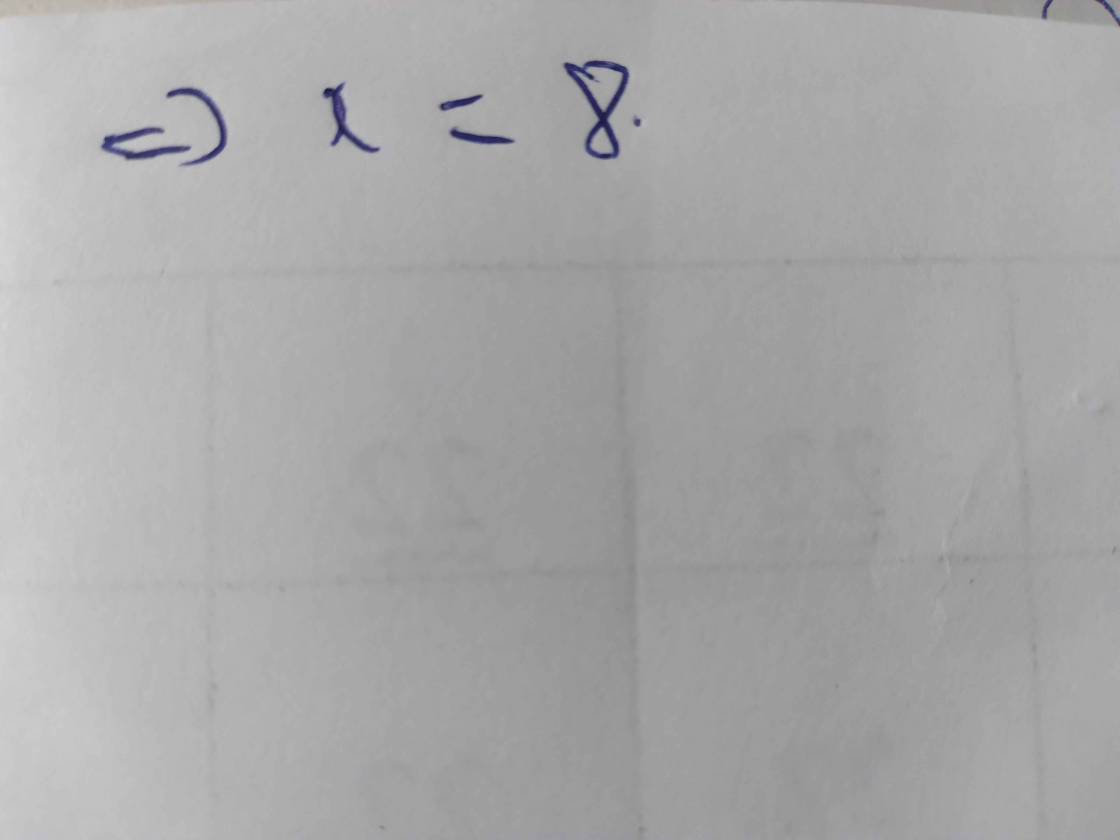
x25y ⋮ 2 và 5 ⇔ y = 0
Thay y = 0 ⇒ x250 chia 3 dư 1 ⇔ ( x + 2 + 5 + 0 ) : 3 dư 1
hay ( x + 7 ) : 3 dư 1
⇒ x = 0 hoặc 3
Mà x đứng đầu ⇒ x chỉ có thể bằng 3
Vậy số đó là 3250